欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给出一个区间的集合,请合并所有重叠的区间。
示例 1: 输入: intervals = [[1,3],[2,6],[8,10],[15,18]] 输出: [[1,6],[8,10],[15,18]] 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2: 输入: intervals = [[1,4],[4,5]] 输出: [[1,5]] 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
提示:
- intervals[i][0] <= intervals[i][1]
大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
都可以!
那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
局部最优可以推出全局最优,找不出反例,试试贪心。
那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
有时候贪心就是常识!哈哈
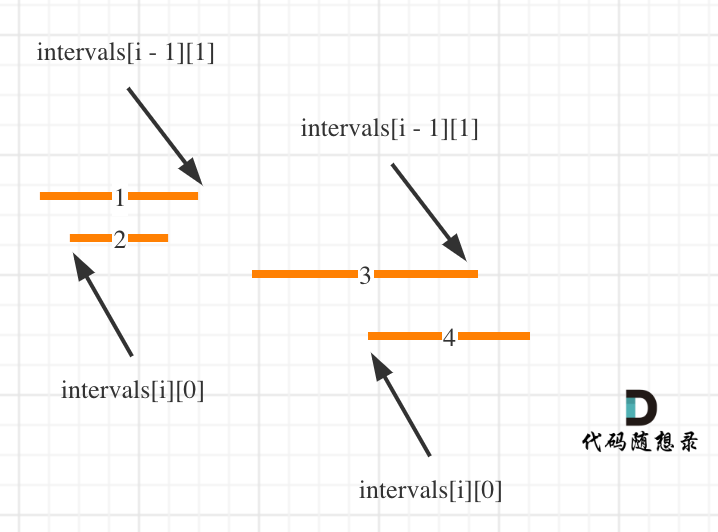
按照左边界从小到大排序之后,如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
这么说有点抽象,看图:(注意图中区间都是按照左边界排序之后了)
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
C++代码如下:
class Solution {
public:
// 按照区间左边界从小到大排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> result;
if (intervals.size() == 0) return result;
sort(intervals.begin(), intervals.end(), cmp);
bool flag = false; // 标记最后一个区间有没有合并
int length = intervals.size();
for (int i = 1; i < length; i++) {
int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
int end = intervals[i - 1][1]; // 初始i-1区间的右边界
while (i < length && intervals[i][0] <= end) { // 合并区间
end = max(end, intervals[i][1]); // 不断更新右区间
if (i == length - 1) flag = true; // 最后一个区间也合并了
i++; // 继续合并下一个区间
}
// start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
result.push_back({start, end});
}
// 如果最后一个区间没有合并,将其加入result
if (flag == false) {
result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
}
return result;
}
};当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> result;
if (intervals.size() == 0) return result;
// 排序的参数使用了lamda表达式
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});
result.push_back(intervals[0]);
for (int i = 1; i < intervals.size(); i++) {
if (result.back()[1] >= intervals[i][0]) { // 合并区间
result.back()[1] = max(result.back()[1], intervals[i][1]);
} else {
result.push_back(intervals[i]);
}
}
return result;
}
};- 时间复杂度:O(nlogn) ,有一个快排
- 空间复杂度:O(1),我没有算result数组(返回值所需容器占的空间)
对于贪心算法,很多同学都是:如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了。
跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
那应该怎么办呢?
正如我贪心系列开篇词关于贪心算法,你该了解这些!中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
Java:
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new LinkedList<>();
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
int start = intervals[0][0];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] > intervals[i - 1][1]) {
res.add(new int[]{start, intervals[i - 1][1]});
start = intervals[i][0];
} else {
intervals[i][1] = Math.max(intervals[i][1], intervals[i - 1][1]);
}
}
res.add(new int[]{start, intervals[intervals.length - 1][1]});
return res.toArray(new int[res.size()][]);
}
}// 版本2
class Solution {
public int[][] merge(int[][] intervals) {
LinkedList<int[]> res = new LinkedList<>();
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] <= res.getLast()[1]) {
int start = res.getLast()[0];
int end = Math.max(intervals[i][1], res.getLast()[1]);
res.removeLast();
res.add(new int[]{start, end});
}
else {
res.add(intervals[i]);
}
}
return res.toArray(new int[res.size()][]);
}
}Python:
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
if len(intervals) == 0: return intervals
intervals.sort(key=lambda x: x[0])
result = []
result.append(intervals[0])
for i in range(1, len(intervals)):
last = result[-1]
if last[1] >= intervals[i][0]:
result[-1] = [last[0], max(last[1], intervals[i][1])]
else:
result.append(intervals[i])
return resultGo:
func merge(intervals [][]int) [][]int {
//先从小到大排序
sort.Slice(intervals,func(i,j int)bool{
return intervals[i][0]<intervals[j][0]
})
//再弄重复的
for i:=0;i<len(intervals)-1;i++{
if intervals[i][1]>=intervals[i+1][0]{
intervals[i][1]=max(intervals[i][1],intervals[i+1][1])//赋值最大值
intervals=append(intervals[:i+1],intervals[i+2:]...)
i--
}
}
return intervals
}
func max(a,b int)int{
if a>b{
return a
}
return b
}Javascript:
var merge = function (intervals) {
intervals.sort((a, b) => a[0] - b[0]);
let prev = intervals[0]
let result = []
for(let i =0; i<intervals.length; i++){
let cur = intervals[i]
if(cur[0] > prev[1]){
result.push(prev)
prev = cur
}else{
prev[1] = Math.max(cur[1],prev[1])
}
}
result.push(prev)
return result
};