diff --git a/README.md b/README.md
index 5a4cc32..50bffaf 100644
--- a/README.md
+++ b/README.md
@@ -1,171 +1,335 @@
-# Coming Version: An SVDD BaseEstimator based on sklearn.base
-
+
+  +
+
--------------------------------------------------------------------
+Support Vector Data Description (SVDD)
+Python code for abnormal detection or fault detection using Support Vector Data Description (SVDD)
+Version 1.1, 11-NOV-2021
+Email: iqiukp@outlook.com
-# Support Vector Data Description (SVDD)
+
-Python Code for abnormal detection or fault detection using SVDD.
-
-Email: iqiukp@outlook.com
+

+

+

+

+

+

+
## Main features
-* SVDD model for training dataset containing only positive training data. (SVDD)
-* SVDD model for training dataset containing both positive training data and negative training data. (nSVDD)
-* Multiple kinds of kernel functions.
-* Visualization module including ROC curve plotting, test result plotting, and decision boundary.
-
--------------------------------------------------------------------
+- SVDD BaseEstimator based on sklearn.base for one-class or binary classification
+- Multiple kinds of kernel functions (linear, gaussian, polynomial, sigmoid)
+- Visualization of decision boundaries for 2D data
## Requirements
-* matplotlib
-* cvxopt
-* scipy
-* numpy
-* scikit_learn
+- cvxopt
+- matplotlib
+- numpy
+- scikit_learn
+- scikit-opt (optional, only used for parameter optimization)
--------------------------------------------------------------------
+## Notices
-## About SVDD model
+- The label must be 1 for positive sample or -1 for negative sample.
+- Detailed applications please see the examples.
+- This code is for reference only.
-Two types of SVDD models are built according to the following references:
+## Examples
-[1] Tax D M J, Duin R P W. Support vector data description[J]. Machine learning, 2004, 54(1): 45-66.
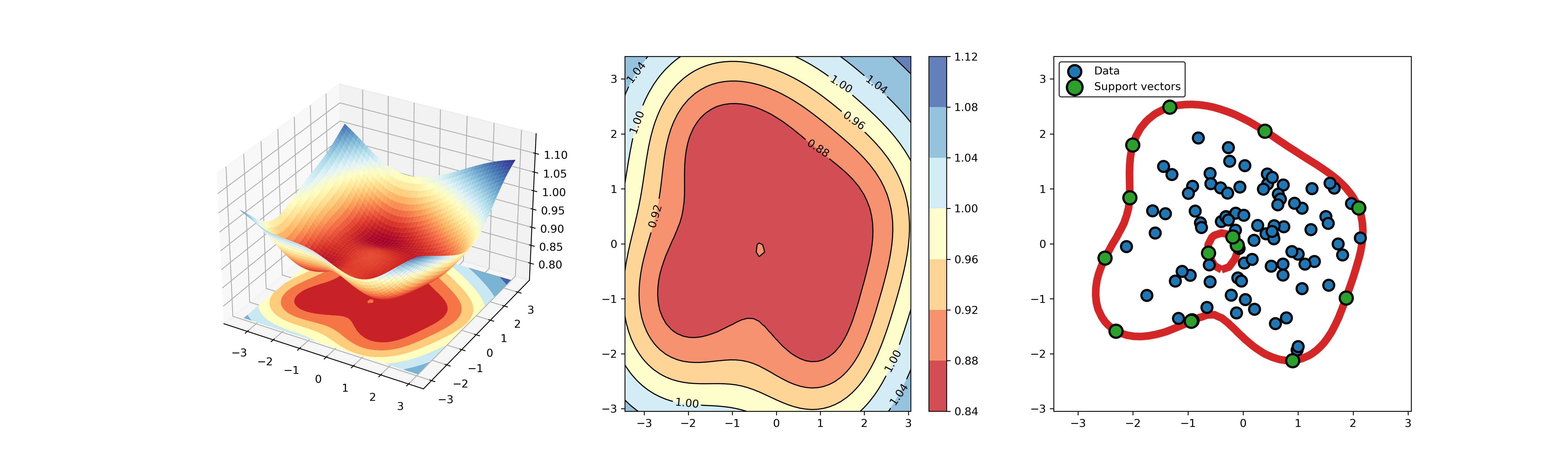
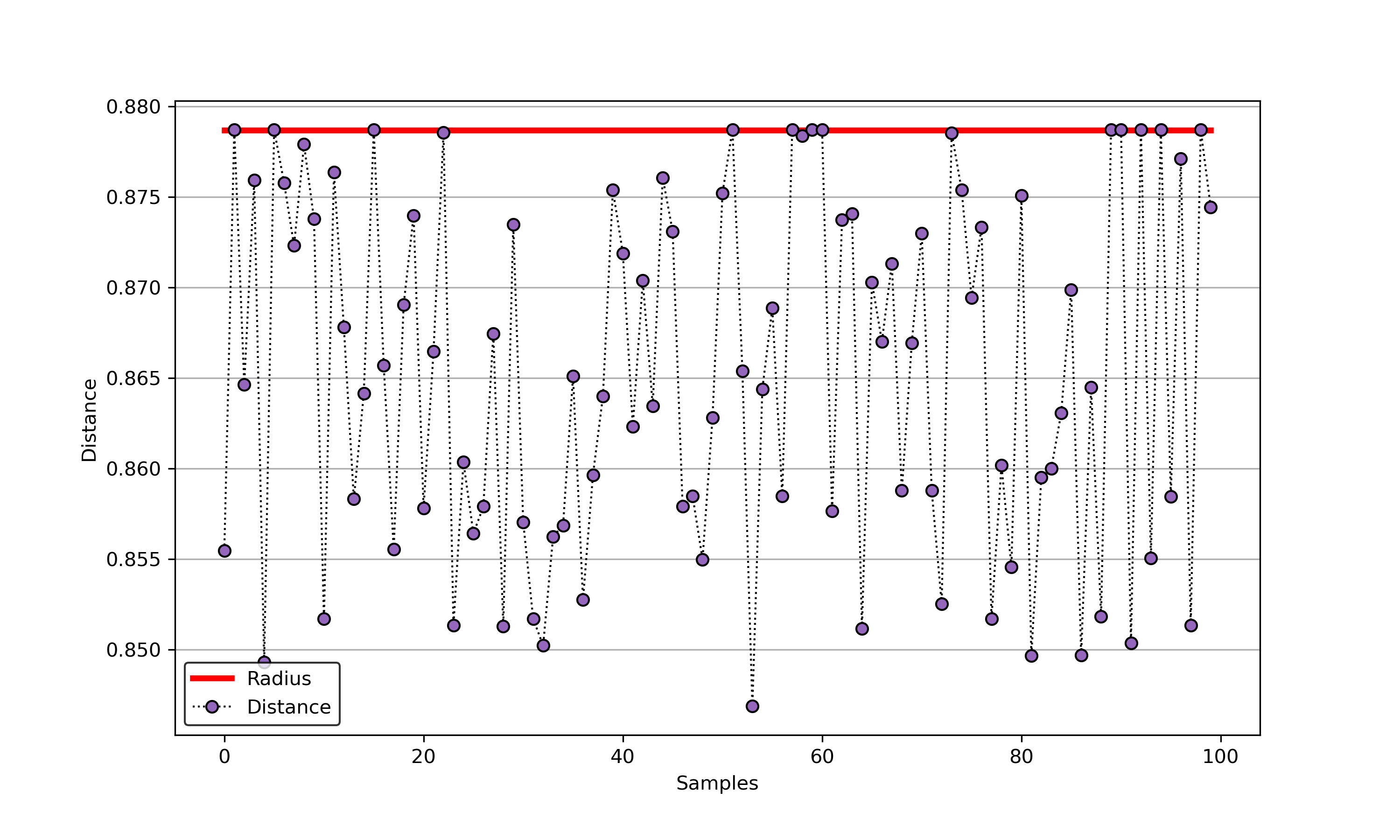
+### 01. svdd_example_unlabeled_data.py
--------------------------------------------------------------------
+An example for SVDD model fitting using unlabeled data.
-## A simple application for decision boundary (using differnent kernel functions)
+
+  +
+  +
+
-```
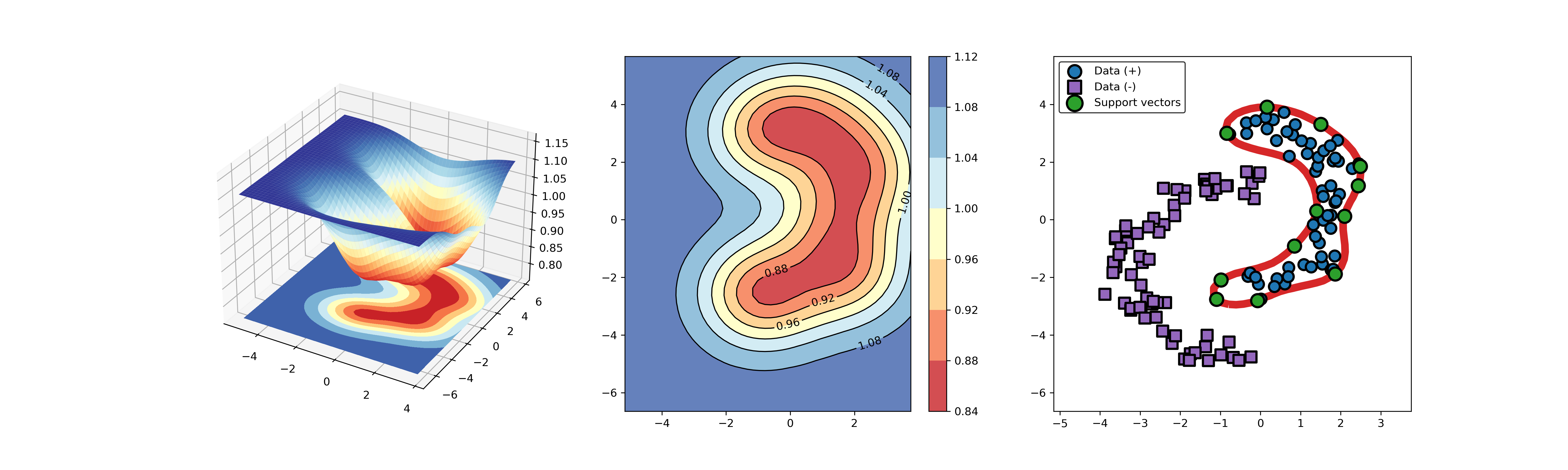
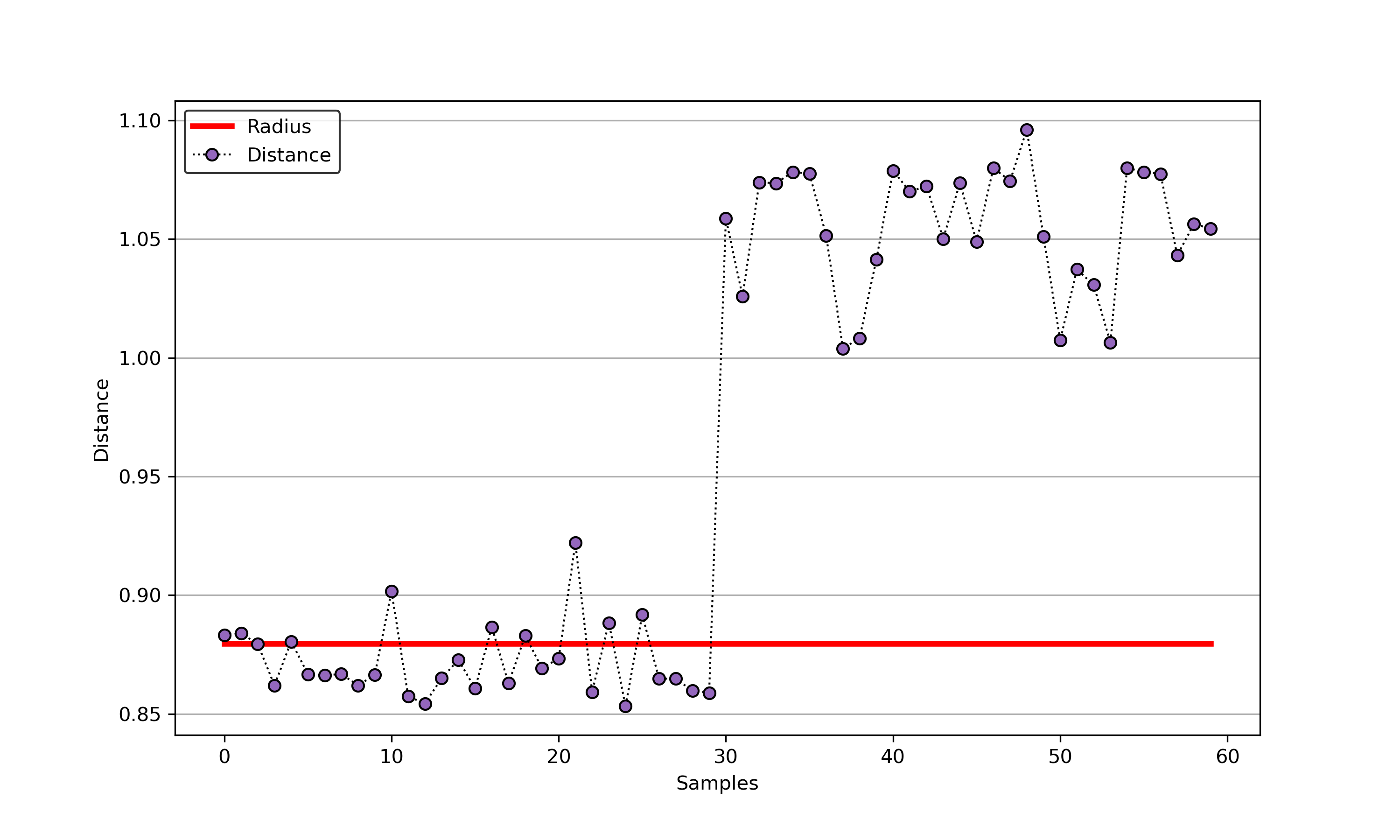
+### 02. svdd_example_hybrid_data.py
-# -*- coding: utf-8 -*-
+An example for SVDD model fitting with negataive samples.
+```
import sys
sys.path.append("..")
-from src.svdd import SVDD
-from src.visualize import Visualization as draw
-from data import PrepareData as load
+from sklearn.datasets import load_wine
+from src.BaseSVDD import BaseSVDD, BananaDataset
+
+# Banana-shaped dataset generation and partitioning
+X, y = BananaDataset.generate(number=100, display='on')
+X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3)
+
+#
+svdd = BaseSVDD(C=0.9, gamma=0.3, kernel='rbf', display='on')
+
+#
+svdd.fit(X_train, y_train)
+
+#
+svdd.plot_boundary(X_train, y_train)
+
+#
+y_test_predict = svdd.predict(X_test, y_test)
+
+#
+radius = svdd.radius
+distance = svdd.get_distance(X_test)
+svdd.plot_distance(radius, distance)
+```
+
+
+  +
+  +
+
-# load banana-shape data
-trainData, testData, trainLabel, testLabel = load.banana()
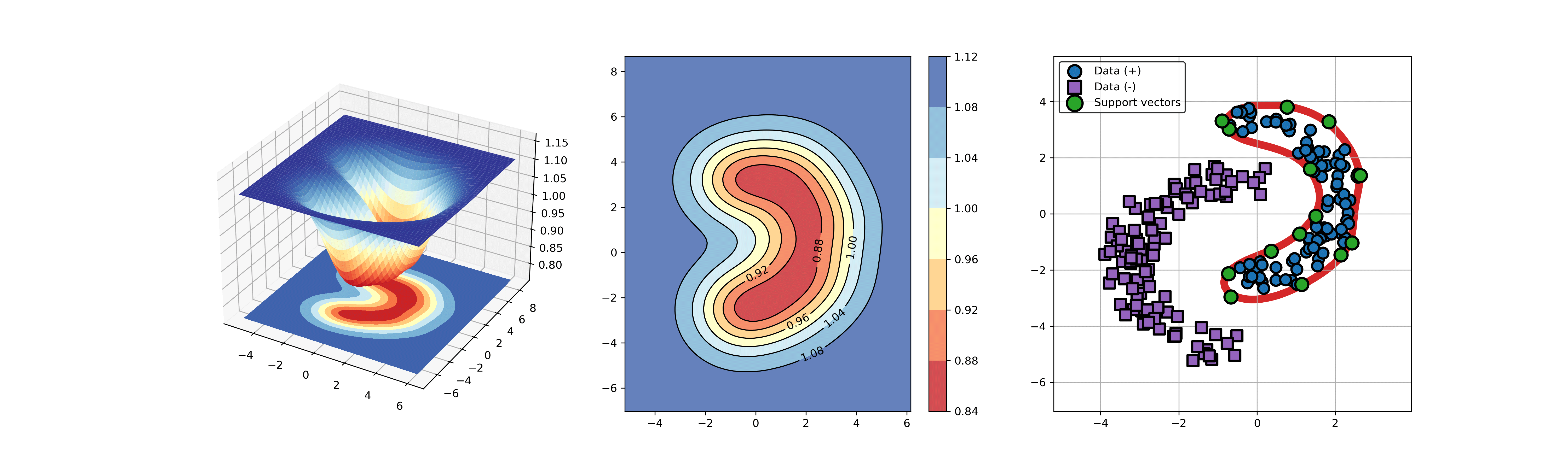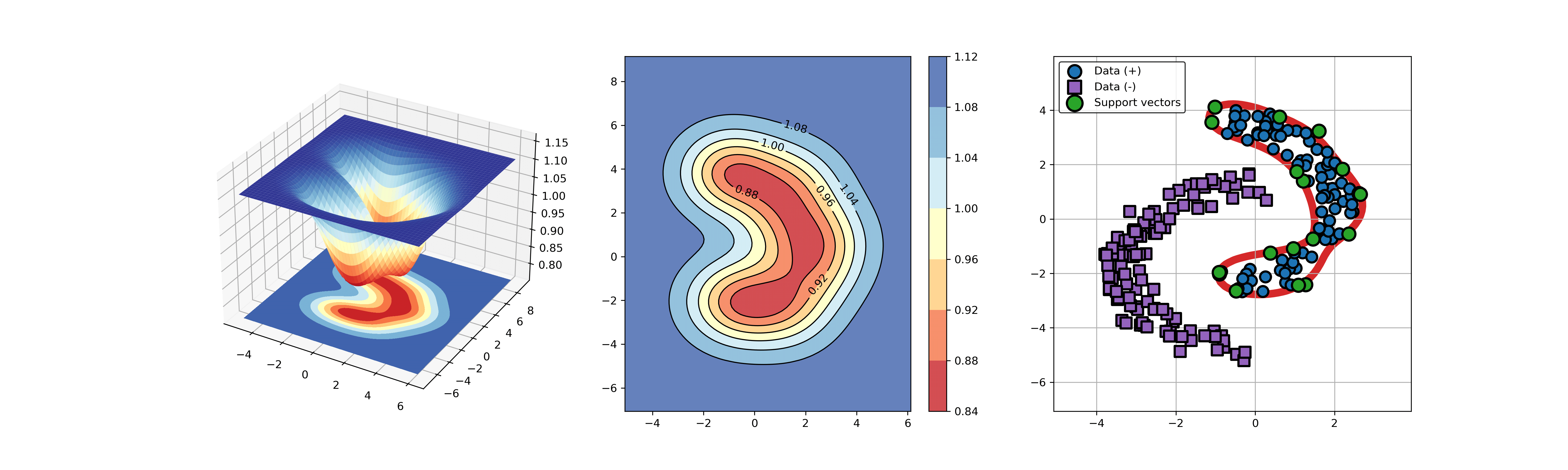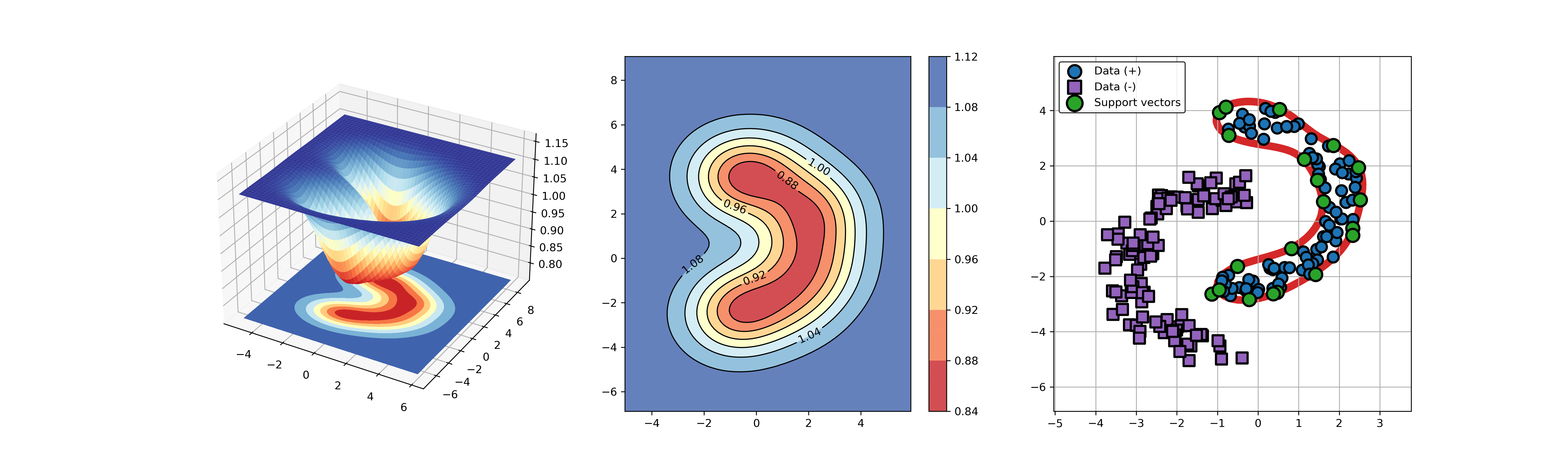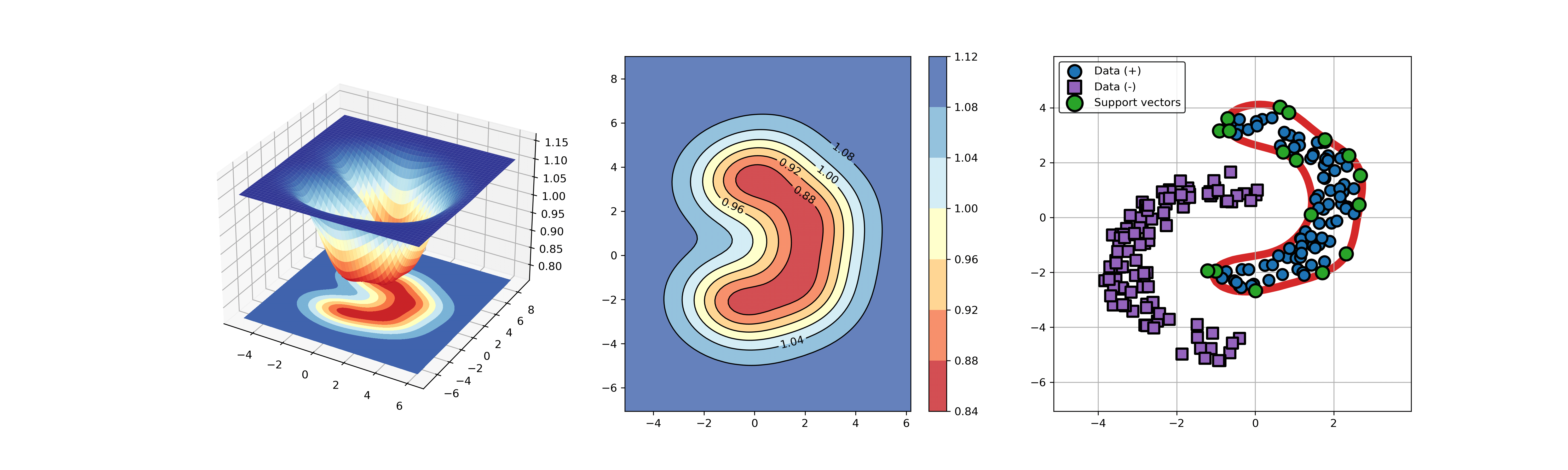
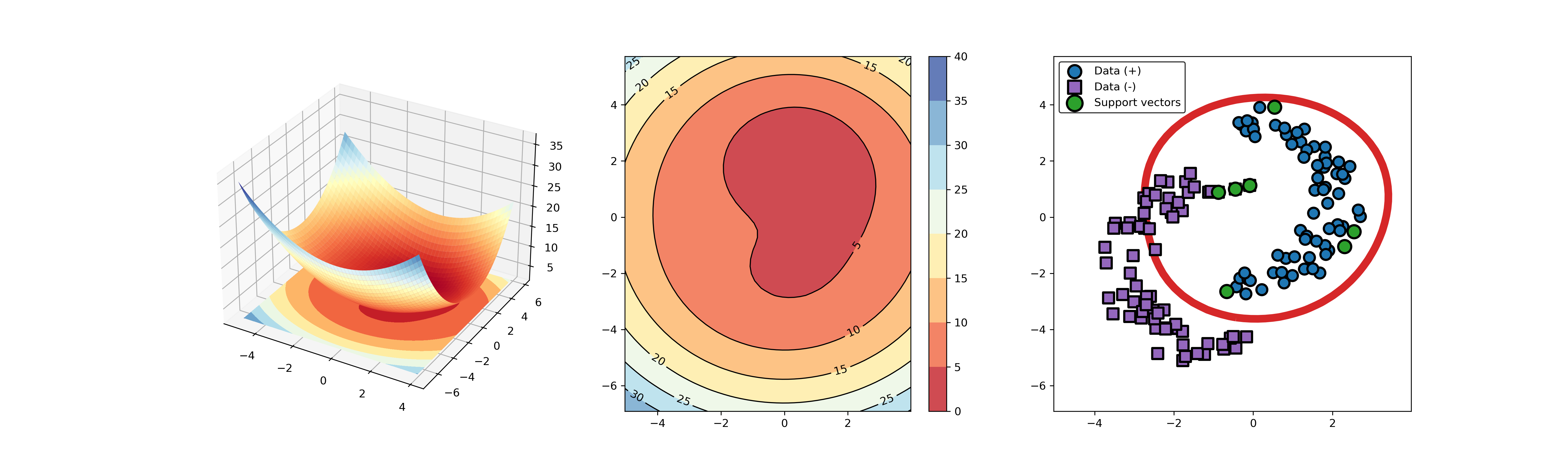
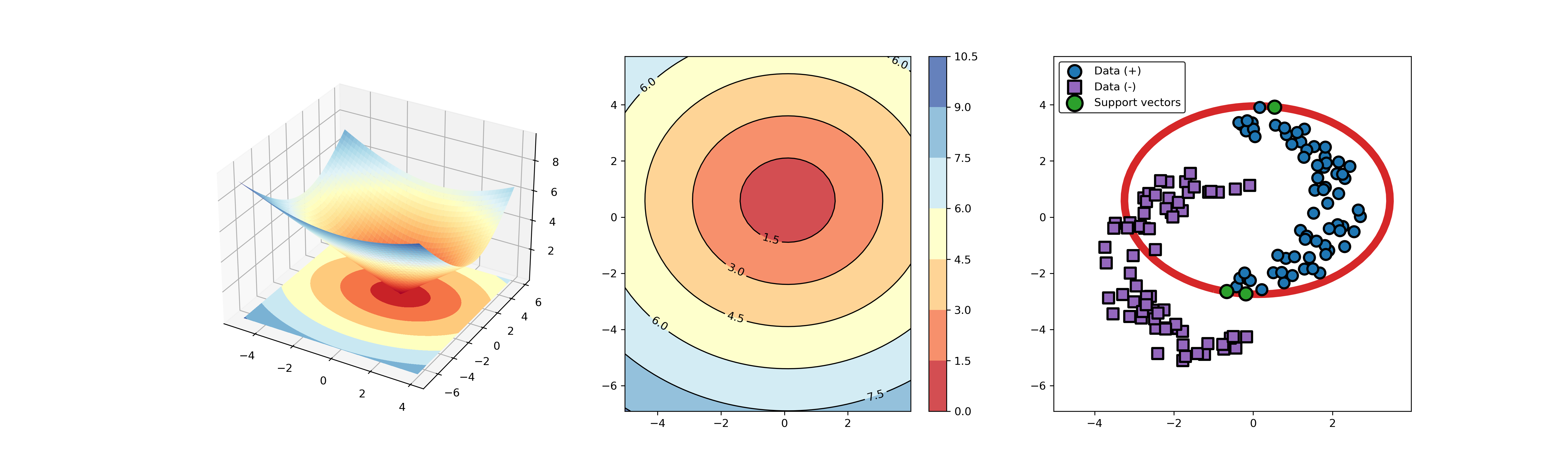
+### 03. svdd_example_kernel.py
+An example for SVDD model fitting using different kernels.
+
+```
+import sys
+sys.path.append("..")
+from src.BaseSVDD import BaseSVDD, BananaDataset
+
+# Banana-shaped dataset generation and partitioning
+X, y = BananaDataset.generate(number=100, display='on')
+X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3)
# kernel list
-kernelList = {"1": {"type": 'gauss', "width": 1/24},
- "2": {"type": 'linear', "offset": 0},
- "3": {"type": 'ploy', "degree": 2, "offset": 0},
- "4": {"type": 'tanh', "gamma": 1e-4, "offset": 0},
- "5": {"type": 'lapl', "width": 1/12}
+kernelList = {"1": BaseSVDD(C=0.9, kernel='rbf', gamma=0.3, display='on'),
+ "2": BaseSVDD(C=0.9, kernel='poly',degree=2, display='on'),
+ "3": BaseSVDD(C=0.9, kernel='linear', display='on')
}
-
+#
for i in range(len(kernelList)):
+ svdd = kernelList.get(str(i+1))
+ svdd.fit(X_train, y_train)
+ svdd.plot_boundary(X_train, y_train)
+```
- # set SVDD parameters
- parameters = {"positive penalty": 0.9,
- "negative penalty": 0.8,
- "kernel": kernelList.get(str(i+1)),
- "option": {"display": 'on'}}
-
- # construct an SVDD model
- svdd = SVDD(parameters)
-
- # train SVDD model
- svdd.train(trainData, trainLabel)
-
- # test SVDD model
- distance, accuracy = svdd.test(testData, testLabel)
-
- # visualize the results
- # draw.testResult(svdd, distance)
- # draw.testROC(testLabel, distance)
- draw.boundary(svdd, trainData, trainLabel)
-
-```
-
-* gaussian kernel function
-
-
-  +
+
+  +
+  +
+ 
-* linear kernel function
-
-  -
-
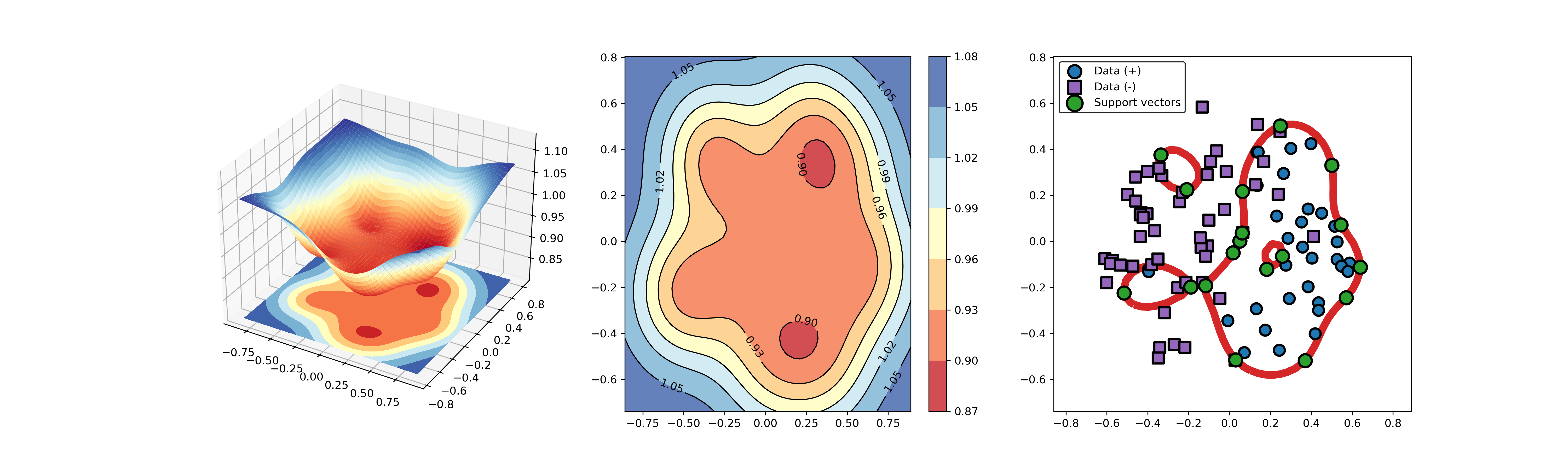
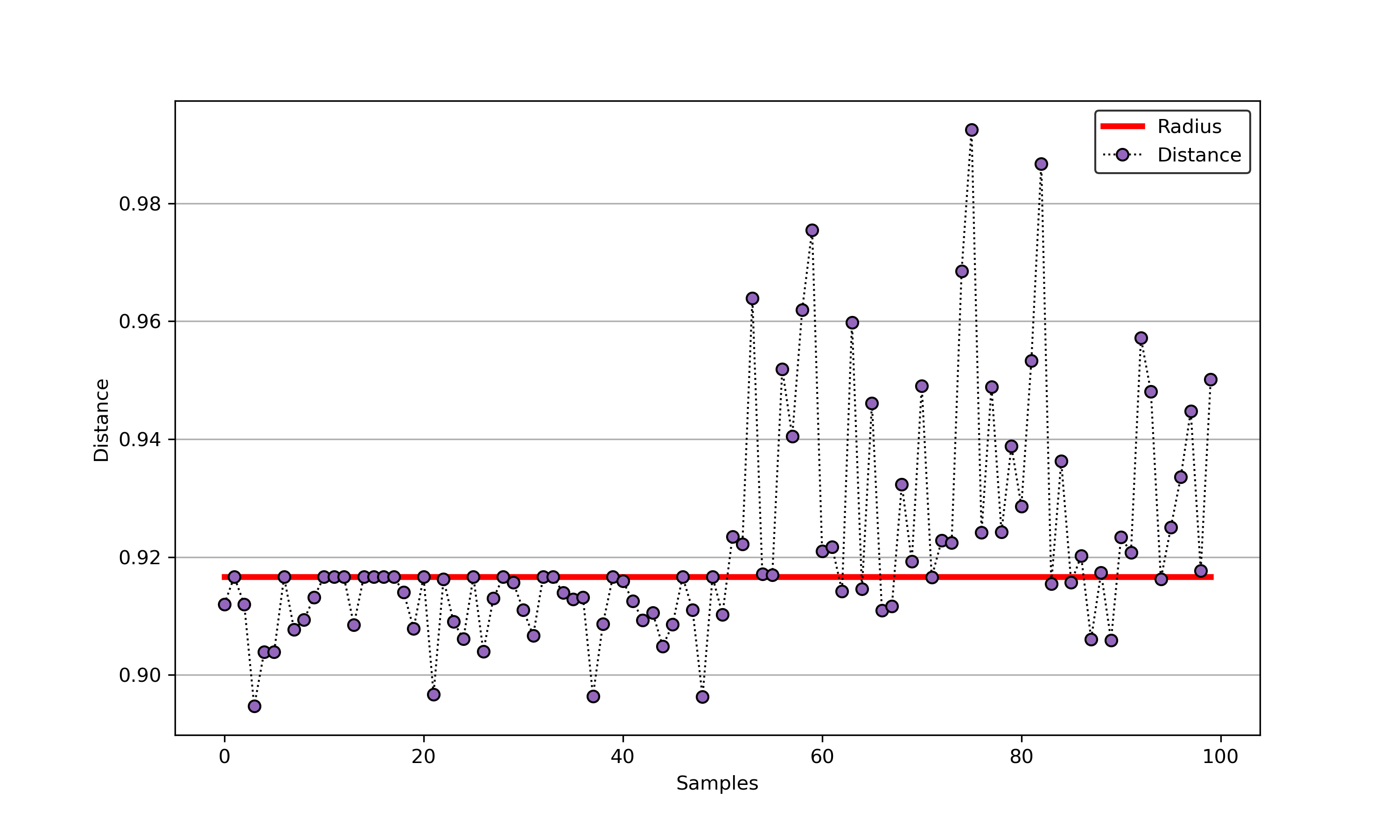
+### 04. svdd_example_KPCA.py
-* polynomial kernel function
+An example for SVDD model fitting using nonlinear principal component.
-
-  -
-
+The KPCA algorithm is used to reduce the dimension of the original data.
-* sigmoid kernel function
+```
+import sys
+sys.path.append("..")
+import numpy as np
+from src.BaseSVDD import BaseSVDD
+from sklearn.decomposition import KernelPCA
-
-  -
-
-* laplacian kernel function
+# create 100 points with 5 dimensions
+X = np.r_[np.random.randn(50, 5) + 1, np.random.randn(50, 5)]
+y = np.append(np.ones((50, 1), dtype=np.int64),
+ -np.ones((50, 1), dtype=np.int64),
+ axis=0)
-
-  -
-
+# number of the dimensionality
+kpca = KernelPCA(n_components=2, kernel="rbf", gamma=0.1, fit_inverse_transform=True)
+X_kpca = kpca.fit_transform(X)
+# fit the SVDD model
+svdd = BaseSVDD(C=0.9, gamma=10, kernel='rbf', display='on')
-## A simple application for abnormal detection or fault detection
+# fit and predict
+svdd.fit(X_kpca, y)
+y_test_predict = svdd.predict(X_kpca, y)
+# plot the distance curve
+radius = svdd.radius
+distance = svdd.get_distance(X_kpca)
+svdd.plot_distance(radius, distance)
+
+# plot the boundary
+svdd.plot_boundary(X_kpca, y)
```
-# -*- coding: utf-8 -*-
+
+  +
+  +
+
+
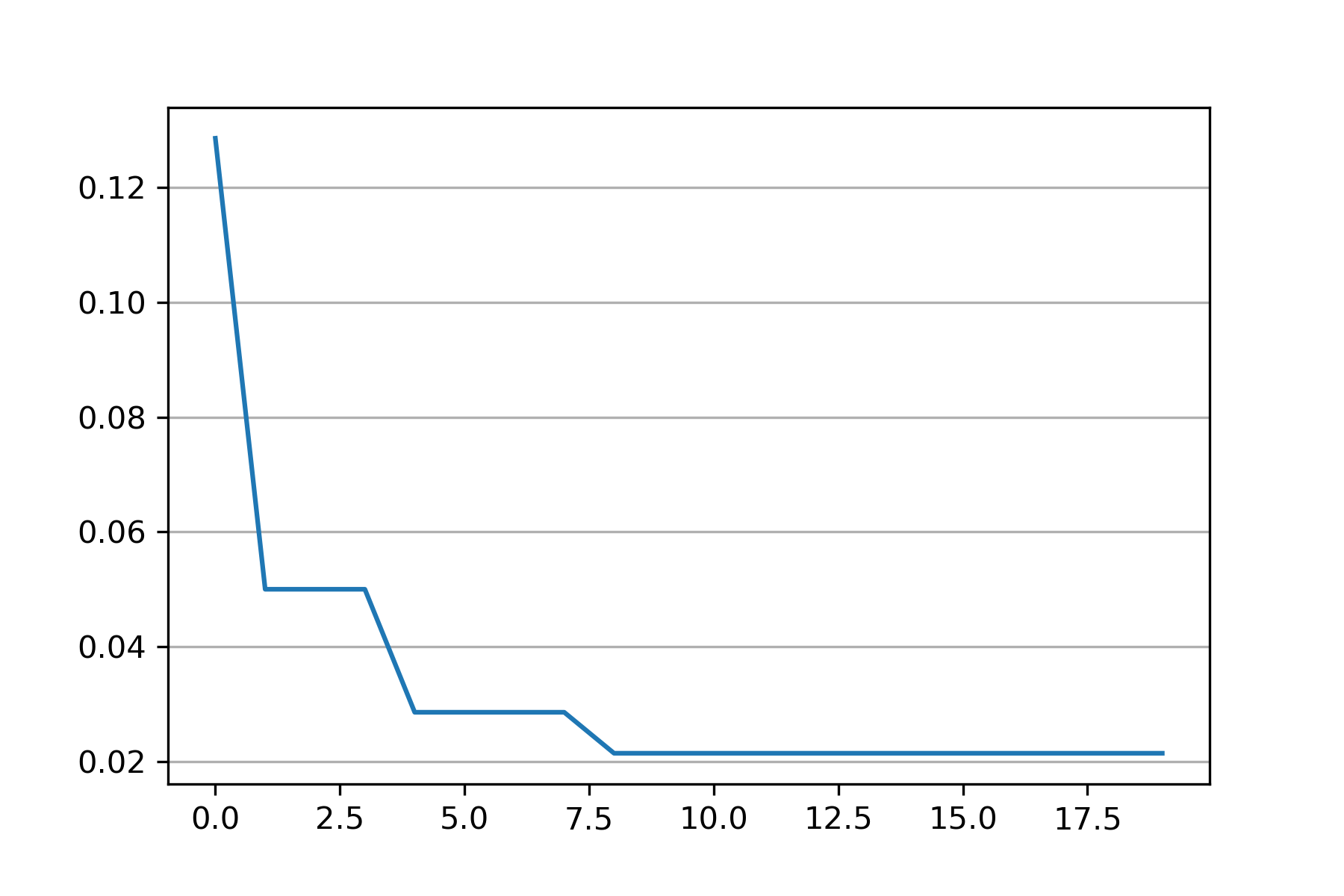
+### 05. svdd_example_PSO.py
+
+An example for parameter optimization using PSO.
+"scikit-opt" is required in this example.
+
+https://github.com/guofei9987/scikit-opt
+
+
+```
import sys
sys.path.append("..")
-from src.svdd import SVDD
-from src.visualize import Visualization as draw
-from data import PrepareData as load
+from src.BaseSVDD import BaseSVDD, BananaDataset
+from sko.PSO import PSO
+import matplotlib.pyplot as plt
+
+
+# Banana-shaped dataset generation and partitioning
+X, y = BananaDataset.generate(number=100, display='off')
+X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3)
+
+# objective function
+def objective_func(x):
+ x1, x2 = x
+ svdd = BaseSVDD(C=x1, gamma=x2, kernel='rbf', display='off')
+ y = 1-svdd.fit(X_train, y_train).accuracy
+ return y
+
+# Do PSO
+pso = PSO(func=objective_func, n_dim=2, pop=10, max_iter=20,
+ lb=[0.01, 0.01], ub=[1, 3], w=0.8, c1=0.5, c2=0.5)
+pso.run()
+
+print('best_x is', pso.gbest_x)
+print('best_y is', pso.gbest_y)
+
+# plot the result
+fig = plt.figure(figsize=(6, 4))
+ax = fig.add_subplot(1, 1, 1)
+ax.plot(pso.gbest_y_hist)
+ax.yaxis.grid()
+plt.show()
+```
-# load banana-shape data
-trainData, testData, trainLabel, testLabel = load.iris()
+
+  +
+
-# set SVDD parameters
-parameters = {"positive penalty": 0.9,
- "negative penalty": 0.8,
- "kernel": {"type": 'gauss', "width": 1/24},
- "option": {"display": 'on'}}
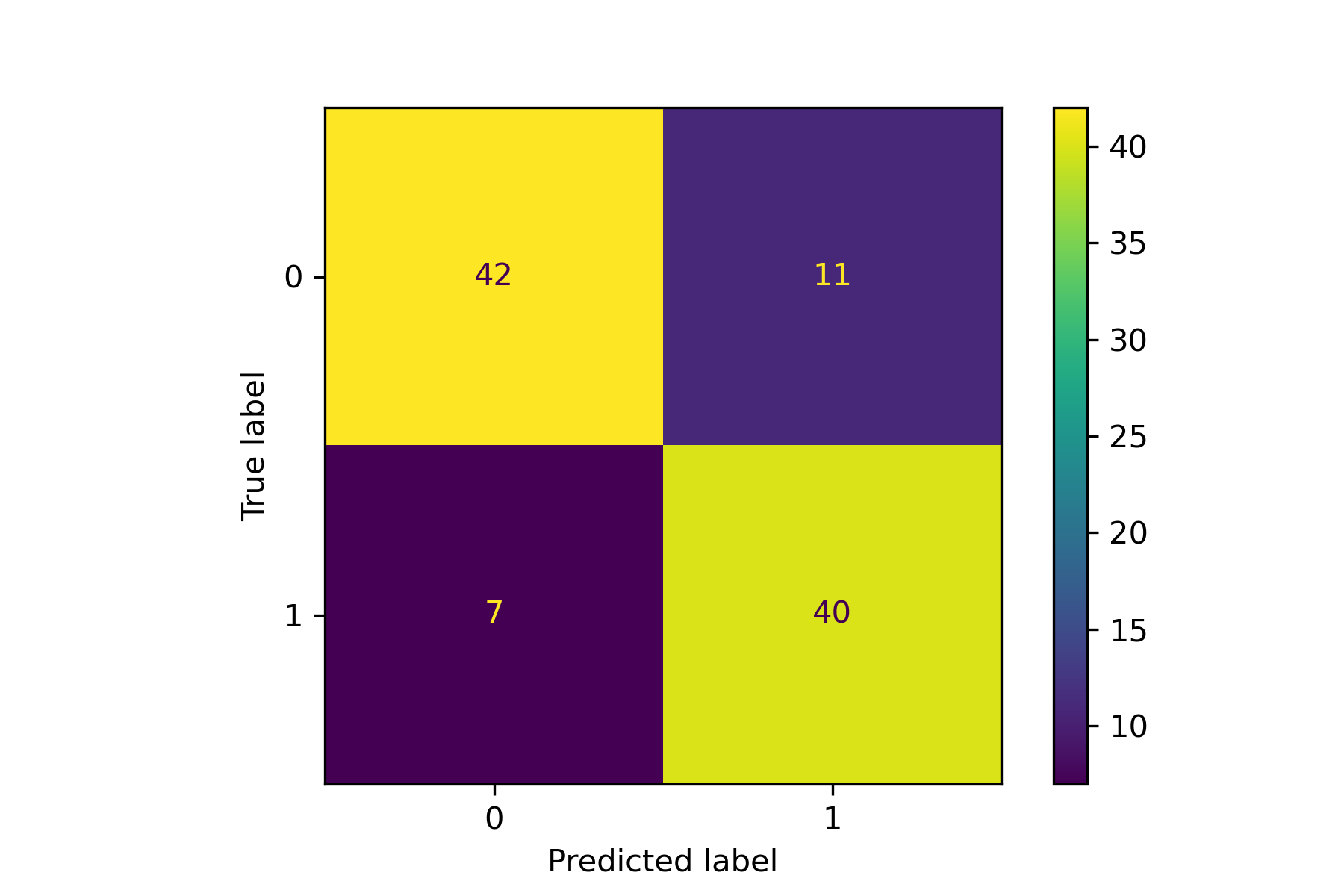
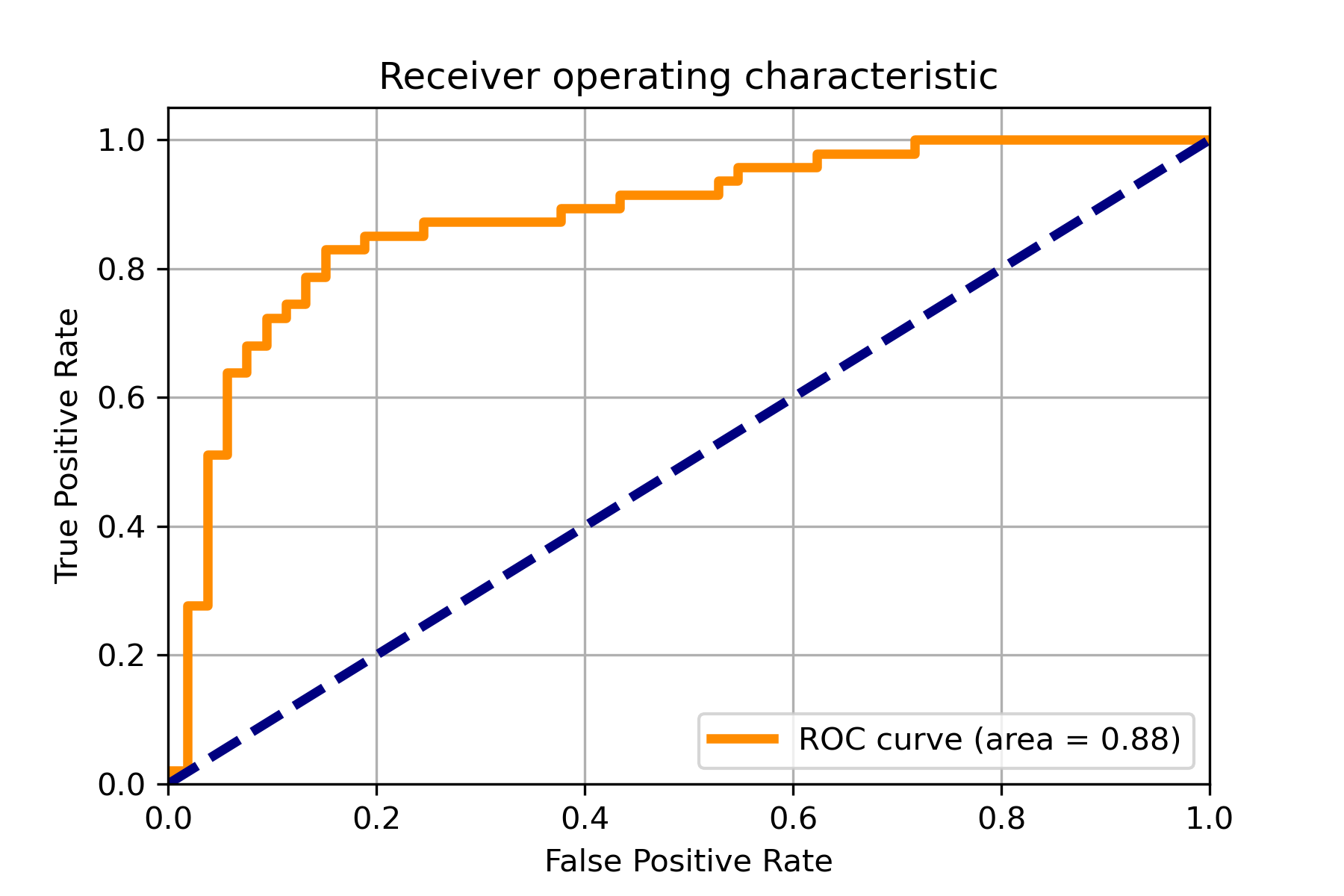
+### 06. svdd_example_confusion_matrix.py
+An example for drawing the confusion matrix and ROC curve.
-# construct an SVDD model
-svdd = SVDD(parameters)
+
+  +
+  +
+
-# train SVDD model
-svdd.train(trainData, trainLabel)
+### 07. svdd_example_cross_validation.py
+An example for cross validation.
-# test SVDD model
-distance, accuracy = svdd.test(testData, testLabel)
+```
+import sys
+sys.path.append("..")
+from src.BaseSVDD import BaseSVDD, BananaDataset
+from sklearn.model_selection import cross_val_score
-# visualize the results
-draw.testResult(svdd, distance)
-draw.testROC(testLabel, distance)
-```
+# Banana-shaped dataset generation and partitioning
+X, y = BananaDataset.generate(number=100, display='on')
+X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3)
-* test result
+#
+svdd = BaseSVDD(C=0.9, gamma=0.3, kernel='rbf', display='on')
-
-  -
-
-* ROC curve
+# cross validation (k-fold)
+k = 5
+scores = cross_val_score(svdd, X_train, y_train, cv=k, scoring='accuracy')
-
-  -
-
+#
+print("Cross validation scores:")
+for scores_ in scores:
+ print(scores_)
+
+print("Mean cross validation score: {:4f}".format(scores.mean()))
+```
+Results
+```
+Cross validation scores:
+0.5714285714285714
+0.75
+0.9642857142857143
+1.0
+1.0
+Mean cross validation score: 0.857143
+```
+
+### 08. svdd_example_grid_search.py
+
+An example for parameter selection using grid search.
+```
+import sys
+sys.path.append("..")
+from sklearn.datasets import load_wine
+from src.BaseSVDD import BaseSVDD, BananaDataset
+from sklearn.model_selection import KFold, LeaveOneOut, ShuffleSplit
+from sklearn.model_selection import learning_curve, GridSearchCV
+
+# Banana-shaped dataset generation and partitioning
+X, y = BananaDataset.generate(number=100, display='off')
+X_train, X_test, y_train, y_test = BananaDataset.split(X, y, ratio=0.3)
+
+param_grid = [
+ {"kernel": ["rbf"], "gamma": [0.1, 0.2, 0.5], "C": [0.1, 0.5, 1]},
+ {"kernel": ["linear"], "C": [0.1, 0.5, 1]},
+ {"kernel": ["poly"], "C": [0.1, 0.5, 1], "degree": [2, 3, 4, 5]},
+]
+
+svdd = GridSearchCV(BaseSVDD(display='off'), param_grid, cv=5, scoring="accuracy")
+svdd.fit(X_train, y_train)
+print("best parameters:")
+print(svdd.best_params_)
+print("\n")
+
+#
+best_model = svdd.best_estimator_
+means = svdd.cv_results_["mean_test_score"]
+stds = svdd.cv_results_["std_test_score"]
+
+for mean, std, params in zip(means, stds, svdd.cv_results_["params"]):
+ print("%0.3f (+/-%0.03f) for %r" % (mean, std * 2, params))
+print()
+
+```
+Results
+```
+best parameters:
+{'C': 0.5, 'gamma': 0.1, 'kernel': 'rbf'}
+
+
+0.921 (+/-0.159) for {'C': 0.1, 'gamma': 0.1, 'kernel': 'rbf'}
+0.893 (+/-0.192) for {'C': 0.1, 'gamma': 0.2, 'kernel': 'rbf'}
+0.857 (+/-0.296) for {'C': 0.1, 'gamma': 0.5, 'kernel': 'rbf'}
+0.950 (+/-0.086) for {'C': 0.5, 'gamma': 0.1, 'kernel': 'rbf'}
+0.921 (+/-0.131) for {'C': 0.5, 'gamma': 0.2, 'kernel': 'rbf'}
+0.864 (+/-0.273) for {'C': 0.5, 'gamma': 0.5, 'kernel': 'rbf'}
+0.950 (+/-0.086) for {'C': 1, 'gamma': 0.1, 'kernel': 'rbf'}
+0.921 (+/-0.131) for {'C': 1, 'gamma': 0.2, 'kernel': 'rbf'}
+0.864 (+/-0.273) for {'C': 1, 'gamma': 0.5, 'kernel': 'rbf'}
+0.807 (+/-0.246) for {'C': 0.1, 'kernel': 'linear'}
+0.821 (+/-0.278) for {'C': 0.5, 'kernel': 'linear'}
+0.793 (+/-0.273) for {'C': 1, 'kernel': 'linear'}
+0.879 (+/-0.184) for {'C': 0.1, 'degree': 2, 'kernel': 'poly'}
+0.836 (+/-0.305) for {'C': 0.1, 'degree': 3, 'kernel': 'poly'}
+0.771 (+/-0.416) for {'C': 0.1, 'degree': 4, 'kernel': 'poly'}
+0.757 (+/-0.448) for {'C': 0.1, 'degree': 5, 'kernel': 'poly'}
+0.871 (+/-0.224) for {'C': 0.5, 'degree': 2, 'kernel': 'poly'}
+0.814 (+/-0.311) for {'C': 0.5, 'degree': 3, 'kernel': 'poly'}
+0.800 (+/-0.390) for {'C': 0.5, 'degree': 4, 'kernel': 'poly'}
+0.764 (+/-0.432) for {'C': 0.5, 'degree': 5, 'kernel': 'poly'}
+0.871 (+/-0.224) for {'C': 1, 'degree': 2, 'kernel': 'poly'}
+0.850 (+/-0.294) for {'C': 1, 'degree': 3, 'kernel': 'poly'}
+0.800 (+/-0.390) for {'C': 1, 'degree': 4, 'kernel': 'poly'}
+0.771 (+/-0.416) for {'C': 1, 'degree': 5, 'kernel': 'poly'}
+```
 +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+  +
+ +
+  +
+ +
+ +
+  +
+ 
 -
- -
- -
- -
- +
+  +
+ +
+ +
+  +
+ -
- -
-