diff --git a/convert/Git.md b/convert/Git.md index 9b8db56..da882fe 100644 --- a/convert/Git.md +++ b/convert/Git.md @@ -8,6 +8,8 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF Git 属于分布式版本控制系统，而 SVN 属于集中式。 +
+ 集中式版本控制只有中心服务器拥有一份代码，而分布式版本控制每个人的电脑上就有一份完整的代码。 集中式版本控制有安全性问题，当中心服务器挂了所有人都没办法工作了。 @@ -24,49 +26,49 @@ Github 就是一个中心服务器。 # 工作流 -
- 新建一个仓库之后，当前目录就成为了工作区，工作区下有一个隐藏目录 .git，它属于 Git 的版本库。 -Git 版本库有一个称为 stage 的暂存区，还有自动创建的 master 分支以及指向分支的 HEAD 指针。 +Git 的版本库有一个称为 Stage 的暂存区以及最后的 History 版本库，History 中存有所有分支，使用一个 HEAD 指针指向当前分支。 -
+
- git add files 把文件的修改添加到暂存区 - git commit 把暂存区的修改提交到当前分支，提交之后暂存区就被清空了 - git reset -- files 使用当前分支上的修改覆盖暂存区，用来撤销最后一次 git add files - git checkout -- files 使用暂存区的修改覆盖工作目录，用来撤销本地修改 -
+
可以跳过暂存区域直接从分支中取出修改，或者直接提交修改到分支中。 - git commit -a 直接把所有文件的修改添加到暂存区然后执行提交 - git checkout HEAD -- files 取出最后一次修改，可以用来进行回滚操作 +
+ # 分支实现 使用指针将每个提交连接成一条时间线，HEAD 指针指向当前分支指针。 -
+
新建分支是新建一个指针指向时间线的最后一个节点，并让 HEAD 指针指向新分支表示新分支成为当前分支。 -
+
每次提交只会让当前分支指针向前移动，而其它分支指针不会移动。 -
+
合并分支也只需要改变指针即可。 -
+
# 冲突 当两个分支都对同一个文件的同一行进行了修改，在分支合并时就会产生冲突。 -
+
Git 会使用 <<<<<<< ，======= ，>>>>>>> 标记出不同分支的内容，只需要把不同分支中冲突部分修改成一样就能解决冲突。 @@ -88,7 +90,7 @@ Creating a new branch is quick AND simple. $ git merge --no-ff -m "merge with no-ff" dev ``` -
+
# 分支管理策略 diff --git a/convert/HTTP.md b/convert/HTTP.md index 68b930c..3440a12 100644 --- a/convert/HTTP.md +++ b/convert/HTTP.md @@ -14,7 +14,7 @@ URI 包含 URL 和 URN。 - URL（Uniform Resource Locator，统一资源定位符） - URN（Uniform Resource Name，统一资源名称） -
+
## 请求和响应报文 @@ -597,7 +597,7 @@ HTTP/1.1 使用虚拟主机技术，使得一台服务器拥有多个域名， 使用 SSL 等加密手段，在客户端和服务器之间建立一条安全的通信线路。 -# 六、HTTPs +# 六、HTTPS HTTP 有以下安全性问题： @@ -605,9 +605,9 @@ HTTP 有以下安全性问题： - 不验证通信方的身份，通信方的身份有可能遭遇伪装； - 无法证明报文的完整性，报文有可能遭篡改。 -HTTPs 并不是新协议，而是让 HTTP 先和 SSL（Secure Sockets Layer）通信，再由 SSL 和 TCP 通信，也就是说 HTTPs 使用了隧道进行通信。 +HTTPS 并不是新协议，而是让 HTTP 先和 SSL（Secure Sockets Layer）通信，再由 SSL 和 TCP 通信，也就是说 HTTPS 使用了隧道进行通信。 -通过使用 SSL，HTTPs 具有了加密（防窃听）、认证（防伪装）和完整性保护（防篡改）。 +通过使用 SSL，HTTPS 具有了加密（防窃听）、认证（防伪装）和完整性保护（防篡改）。
@@ -635,9 +635,9 @@ HTTPs 并不是新协议，而是让 HTTP 先和 SSL（Secure Sockets Layer）
-### 3. HTTPs 采用的加密方式 +### 3. HTTPS 采用的加密方式 -HTTPs 采用混合的加密机制，使用非对称密钥加密用于传输对称密钥来保证传输过程的安全性，之后使用对称密钥加密进行通信来保证通信过程的效率。（下图中的 Session Key 就是对称密钥） +HTTPS 采用混合的加密机制，使用非对称密钥加密用于传输对称密钥来保证传输过程的安全性，之后使用对称密钥加密进行通信来保证通信过程的效率。（下图中的 Session Key 就是对称密钥）
@@ -649,7 +649,7 @@ HTTPs 采用混合的加密机制，使用非对称密钥加密用于传输对 服务器的运营人员向 CA 提出公开密钥的申请，CA 在判明提出申请者的身份之后，会对已申请的公开密钥做数字签名，然后分配这个已签名的公开密钥，并将该公开密钥放入公开密钥证书后绑定在一起。 -进行 HTTPs 通信时，服务器会把证书发送给客户端。客户端取得其中的公开密钥之后，先使用数字签名进行验证，如果验证通过，就可以开始通信了。 +进行 HTTPS 通信时，服务器会把证书发送给客户端。客户端取得其中的公开密钥之后，先使用数字签名进行验证，如果验证通过，就可以开始通信了。
@@ -659,9 +659,9 @@ SSL 提供报文摘要功能来进行完整性保护。 HTTP 也提供了 MD5 报文摘要功能，但不是安全的。例如报文内容被篡改之后，同时重新计算 MD5 的值，通信接收方是无法意识到发生了篡改。 -HTTPs 的报文摘要功能之所以安全，是因为它结合了加密和认证这两个操作。试想一下，加密之后的报文，遭到篡改之后，也很难重新计算报文摘要，因为无法轻易获取明文。 +HTTPS 的报文摘要功能之所以安全，是因为它结合了加密和认证这两个操作。试想一下，加密之后的报文，遭到篡改之后，也很难重新计算报文摘要，因为无法轻易获取明文。 -## HTTPs 的缺点 +## HTTPS 的缺点 - 因为需要进行加密解密等过程，因此速度会更慢； - 需要支付证书授权的高额费用。 diff --git a/convert/Java IO.md b/convert/Java IO.md index 007730f..52de7aa 100644 --- a/convert/Java IO.md +++ b/convert/Java IO.md @@ -70,7 +70,7 @@ Java I/O 使用了装饰者模式来实现。以 InputStream 为例， - FileInputStream 是 InputStream 的子类，属于具体组件，提供了字节流的输入操作； - FilterInputStream 属于抽象装饰者，装饰者用于装饰组件，为组件提供额外的功能。例如 BufferedInputStream 为 FileInputStream 提供缓存的功能。 -
+
实例化一个具有缓存功能的字节流对象时，只需要在 FileInputStream 对象上再套一层 BufferedInputStream 对象即可。 @@ -250,7 +250,7 @@ public static void main(String[] args) throws IOException { - Socket：客户端类 - 服务器和客户端通过 InputStream 和 OutputStream 进行输入输出。 -
+
## Datagram @@ -386,7 +386,7 @@ NIO 实现了 IO 多路复用中的 Reactor 模型，一个线程 Thread 使用 应该注意的是，只有套接字 Channel 才能配置为非阻塞，而 FileChannel 不能，为 FileChannel 配置非阻塞也没有意义。 -
+
### 1. 创建选择器 diff --git "a/convert/Java \345\237\272\347\241\200.md" "b/convert/Java \345\237\272\347\241\200.md" index 7a83461..6e43a3b 100644 --- "a/convert/Java \345\237\272\347\241\200.md" +++ "b/convert/Java \345\237\272\347\241\200.md" @@ -6,11 +6,8 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF # 一、数据类型 -## 包装类型 - -八个基本类型： +## 基本类型 -- boolean/1 - byte/8 - char/16 - short/16 @@ -18,6 +15,14 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF - float/32 - long/64 - double/64 +- boolean/\~ + +boolean 只有两个值：true、false，可以使用 1 bit 来存储，但是具体大小没有明确规定。JVM 会在编译时期将 boolean 类型的数据转换为 int，使用 1 来表示 true，0 表示 false。JVM 并不支持 boolean 数组，而是使用 byte 数组来表示 int 数组来表示。 + +- [Primitive Data Types](https://docs.oracle.com/javase/tutorial/java/nutsandbolts/datatypes.html) +- [The Java® Virtual Machine Specification](https://docs.oracle.com/javase/specs/jvms/se8/jvms8.pdf) + +## 包装类型 基本类型都有对应的包装类型，基本类型与其对应的包装类型之间的赋值使用自动装箱与拆箱完成。 @@ -148,7 +153,7 @@ value 数组被声明为 final，这意味着 value 数组初始化之后就不 如果一个 String 对象已经被创建过了，那么就会从 String Pool 中取得引用。只有 String 是不可变的，才可能使用 String Pool。 -
+
**3. 安全性** @@ -640,6 +645,65 @@ SuperExtendExample.func() 应该注意的是，返回值不同，其它都相同不算是重载。 +**3. 实例** + +```java +class A { + public String show(D obj) { + return ("A and D"); + } + + public String show(A obj) { + return ("A and A"); + } +} + +class B extends A { + public String show(B obj) { + return ("B and B"); + } + + public String show(A obj) { + return ("B and A"); + } +} + +class C extends B { +} + +class D extends B { +} +``` + +```java +public class Test { + + public static void main(String[] args) { + A a1 = new A(); + A a2 = new B(); + B b = new B(); + C c = new C(); + D d = new D(); + System.out.println(a1.show(b)); // A and A + System.out.println(a1.show(c)); // A and A + System.out.println(a1.show(d)); // A and D + System.out.println(a2.show(b)); // B and A + System.out.println(a2.show(c)); // B and A + System.out.println(a2.show(d)); // A and D + System.out.println(b.show(b)); // B and B + System.out.println(b.show(c)); // B and B + System.out.println(b.show(d)); // A and D + } +} +``` + +涉及到重写时，方法调用的优先级为： + +- this.show(O) +- super.show(O) +- this.show((super)O) +- super.show((super)O) + # 五、Object 通用方法 ## 概览 diff --git "a/convert/Java \345\256\271\345\231\250.md" "b/convert/Java \345\256\271\345\231\250.md" index 4d69c98..314c02f 100644 --- "a/convert/Java \345\256\271\345\231\250.md" +++ "b/convert/Java \345\256\271\345\231\250.md" @@ -10,7 +10,8 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF ## Collection -
+
+ ### 1. Set @@ -36,7 +37,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF ## Map -
+
- TreeMap：基于红黑树实现。 @@ -51,7 +52,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF ## 迭代器模式 -
+
Collection 继承了 Iterable 接口，其中的 iterator() 方法能够产生一个 Iterator 对象，通过这个对象就可以迭代遍历 Collection 中的元素。 @@ -96,6 +97,7 @@ List list = Arrays.asList(1, 2, 3); ## ArrayList + ### 1. 概览 实现了 RandomAccess 接口，因此支持随机访问。这是理所当然的，因为 ArrayList 是基于数组实现的。 @@ -111,6 +113,9 @@ public class ArrayList extends AbstractList private static final int DEFAULT_CAPACITY = 10; ``` +
+ + ### 2. 扩容 添加元素时使用 ensureCapacityInternal() 方法来保证容量足够，如果不够时，需要使用 grow() 方法进行扩容，新容量的大小为 `oldCapacity + (oldCapacity >> 1)`，也就是旧容量的 1.5 倍。 @@ -372,7 +377,7 @@ transient Node first; transient Node last; ``` -
+
### 2. 与 ArrayList 的比较 @@ -394,7 +399,7 @@ transient Entry[] table; Entry 存储着键值对。它包含了四个字段，从 next 字段我们可以看出 Entry 是一个链表。即数组中的每个位置被当成一个桶，一个桶存放一个链表。HashMap 使用拉链法来解决冲突，同一个链表中存放哈希值相同的 Entry。 -
+
```java static class Entry implements Map.Entry { @@ -470,7 +475,7 @@ map.put("K3", "V3"); - 计算键值对所在的桶； - 在链表上顺序查找，时间复杂度显然和链表的长度成正比。 -
+
### 3. put 操作 @@ -806,7 +811,7 @@ final Segment[] segments; static final int DEFAULT_CONCURRENCY_LEVEL = 16; ``` -
+
### 2. size 操作 @@ -1077,90 +1082,6 @@ public final class ConcurrentCache { } ``` -# 附录 - -Collection 绘图源码： - -``` -@startuml - -interface Collection -interface Set -interface List -interface Queue -interface SortSet - -class HashSet -class LinkedHashSet -class TreeSet -class ArrayList -class Vector -class LinkedList -class PriorityQueue - - -Collection <|-- Set -Collection <|-- List -Collection <|-- Queue -Set <|-- SortSet - -Set <|.. HashSet -Set <|.. LinkedHashSet -SortSet <|.. TreeSet -List <|.. ArrayList -List <|.. Vector -List <|.. LinkedList -Queue <|.. LinkedList -Queue <|.. PriorityQueue - -@enduml -``` - -Map 绘图源码 - -``` -@startuml - -interface Map -interface SortMap - -class HashTable -class LinkedHashMap -class HashMap -class TreeMap - -Map <|.. HashTable -Map <|.. LinkedHashMap -Map <|.. HashMap -Map <|-- SortMap -SortMap <|.. TreeMap - -@enduml -``` - -迭代器类图 - -``` -@startuml - -interface Iterable -interface Collection -interface List -interface Set -interface Queue -interface Iterator -interface ListIterator - -Iterable <|-- Collection -Collection <|.. List -Collection <|.. Set -Collection <|-- Queue -Iterator <-- Iterable -Iterator <|.. ListIterator -ListIterator <-- List - -@enduml -``` # 参考资料 diff --git "a/convert/Java \345\271\266\345\217\221.md" "b/convert/Java \345\271\266\345\217\221.md" index f9208e1..862d713 100644 --- "a/convert/Java \345\271\266\345\217\221.md" +++ "b/convert/Java \345\271\266\345\217\221.md" @@ -6,7 +6,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF # 一、线程状态转换 -
+
## 新建（New） @@ -30,7 +30,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF | --- | --- | | 没有设置 Timeout 参数的 Object.wait() 方法 | Object.notify() / Object.notifyAll() | | 没有设置 Timeout 参数的 Thread.join() 方法 | 被调用的线程执行完毕 | -| LockSupport.park() 方法 | - | +| LockSupport.park() 方法 | LockSupport.unpark(Thread) | ## 限期等待（Timed Waiting） @@ -49,8 +49,8 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF | Thread.sleep() 方法 | 时间结束 | | 设置了 Timeout 参数的 Object.wait() 方法 | 时间结束 / Object.notify() / Object.notifyAll() | | 设置了 Timeout 参数的 Thread.join() 方法 | 时间结束 / 被调用的线程执行完毕 | -| LockSupport.parkNanos() 方法 | - | -| LockSupport.parkUntil() 方法 | - | +| LockSupport.parkNanos() 方法 | LockSupport.unpark(Thread) | +| LockSupport.parkUntil() 方法 | LockSupport.unpark(Thread) | ## 死亡（Terminated） @@ -675,13 +675,13 @@ after java.util.concurrent（J.U.C）大大提高了并发性能，AQS 被认为是 J.U.C 的核心。 -## CountdownLatch +## CountDownLatch 用来控制一个线程等待多个线程。 维护了一个计数器 cnt，每次调用 countDown() 方法会让计数器的值减 1，减到 0 的时候，那些因为调用 await() 方法而在等待的线程就会被唤醒。 -
+
```java public class CountdownLatchExample { @@ -730,7 +730,7 @@ public CyclicBarrier(int parties) { } ``` -
+
```java public class CyclicBarrierExample { @@ -763,8 +763,6 @@ before..before..before..before..before..before..before..before..before..before.. Semaphore 类似于操作系统中的信号量，可以控制对互斥资源的访问线程数。 -
- 以下代码模拟了对某个服务的并发请求，每次只能有 3 个客户端同时访问，请求总数为 10。 ```java @@ -969,7 +967,7 @@ public class ForkJoinPool extends AbstractExecutorService ForkJoinPool 实现了工作窃取算法来提高 CPU 的利用率。每个线程都维护了一个双端队列，用来存储需要执行的任务。工作窃取算法允许空闲的线程从其它线程的双端队列中窃取一个任务来执行。窃取的任务必须是最晚的任务，避免和队列所属线程发生竞争。例如下图中，Thread2 从 Thread1 的队列中拿出最晚的 Task1 任务，Thread1 会拿出 Task2 来执行，这样就避免发生竞争。但是如果队列中只有一个任务时还是会发生竞争。 -
+
# 九、线程不安全示例 @@ -1024,19 +1022,19 @@ Java 内存模型试图屏蔽各种硬件和操作系统的内存访问差异， 加入高速缓存带来了一个新的问题：缓存一致性。如果多个缓存共享同一块主内存区域，那么多个缓存的数据可能会不一致，需要一些协议来解决这个问题。 -
+
所有的变量都存储在主内存中，每个线程还有自己的工作内存，工作内存存储在高速缓存或者寄存器中，保存了该线程使用的变量的主内存副本拷贝。 线程只能直接操作工作内存中的变量，不同线程之间的变量值传递需要通过主内存来完成。 -
+
## 内存间交互操作 Java 内存模型定义了 8 个操作来完成主内存和工作内存的交互操作。 -
+
- read：把一个变量的值从主内存传输到工作内存中 - load：在 read 之后执行，把 read 得到的值放入工作内存的变量副本中 @@ -1059,11 +1057,11 @@ Java 内存模型保证了 read、load、use、assign、store、write、lock 和 下图演示了两个线程同时对 cnt 进行操作，load、assign、store 这一系列操作整体上看不具备原子性，那么在 T1 修改 cnt 并且还没有将修改后的值写入主内存，T2 依然可以读入旧值。可以看出，这两个线程虽然执行了两次自增运算，但是主内存中 cnt 的值最后为 1 而不是 2。因此对 int 类型读写操作满足原子性只是说明 load、assign、store 这些单个操作具备原子性。 -
+
AtomicInteger 能保证多个线程修改的原子性。 -
+
使用 AtomicInteger 重写之前线程不安全的代码之后得到以下线程安全实现： @@ -1171,7 +1169,7 @@ volatile 关键字通过添加内存屏障的方式来禁止指令重排，即 在一个线程内，在程序前面的操作先行发生于后面的操作。 -
+
### 2. 管程锁定规则 @@ -1179,7 +1177,7 @@ volatile 关键字通过添加内存屏障的方式来禁止指令重排，即 一个 unlock 操作先行发生于后面对同一个锁的 lock 操作。 -
+
### 3. volatile 变量规则 @@ -1187,7 +1185,7 @@ volatile 关键字通过添加内存屏障的方式来禁止指令重排，即 对一个 volatile 变量的写操作先行发生于后面对这个变量的读操作。 -
+
### 4. 线程启动规则 @@ -1195,7 +1193,7 @@ volatile 关键字通过添加内存屏障的方式来禁止指令重排，即 Thread 对象的 start() 方法调用先行发生于此线程的每一个动作。 -
+
### 5. 线程加入规则 @@ -1203,7 +1201,7 @@ Thread 对象的 start() 方法调用先行发生于此线程的每一个动作 Thread 对象的结束先行发生于 join() 方法返回。 -
+
### 6. 线程中断规则 @@ -1421,7 +1419,7 @@ public class ThreadLocalExample1 { 它所对应的底层结构图为： -
+
每个 Thread 都有一个 ThreadLocal.ThreadLocalMap 对象。 diff --git "a/convert/Java \350\231\232\346\213\237\346\234\272.md" "b/convert/Java \350\231\232\346\213\237\346\234\272.md" index 4f0c075..d5d404e 100644 --- "a/convert/Java \350\231\232\346\213\237\346\234\272.md" +++ "b/convert/Java \350\231\232\346\213\237\346\234\272.md" @@ -6,7 +6,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF # 一、运行时数据区域 -
+
## 程序计数器 @@ -16,7 +16,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 每个 Java 方法在执行的同时会创建一个栈帧用于存储局部变量表、操作数栈、常量池引用等信息。从方法调用直至执行完成的过程，就对应着一个栈帧在 Java 虚拟机栈中入栈和出栈的过程。 -
+
可以通过 -Xss 这个虚拟机参数来指定每个线程的 Java 虚拟机栈内存大小： @@ -35,20 +35,20 @@ java -Xss512M HackTheJava 本地方法一般是用其它语言（C、C++ 或汇编语言等）编写的，并且被编译为基于本机硬件和操作系统的程序，对待这些方法需要特别处理。 -
+
## 堆 所有对象都在这里分配内存，是垃圾收集的主要区域（"GC 堆"）。 -现代的垃圾收集器基本都是采用分代收集算法，其主要的思想是针对不同类型的对象采取不同的垃圾回收算法，可以将堆分成两块： +现代的垃圾收集器基本都是采用分代收集算法，其主要的思想是针对不同类型的对象采取不同的垃圾回收算法。可以将堆分成两块： - 新生代（Young Generation） - 老年代（Old Generation） 堆不需要连续内存，并且可以动态增加其内存，增加失败会抛出 OutOfMemoryError 异常。 -可以通过 -Xms 和 -Xmx 两个虚拟机参数来指定一个程序的堆内存大小，第一个参数设置初始值，第二个参数设置最大值。 +可以通过 -Xms 和 -Xmx 这两个虚拟机参数来指定一个程序的堆内存大小，第一个参数设置初始值，第二个参数设置最大值。 ```java java -Xms1M -Xmx2M HackTheJava @@ -62,86 +62,78 @@ java -Xms1M -Xmx2M HackTheJava 对这块区域进行垃圾回收的主要目标是对常量池的回收和对类的卸载，但是一般比较难实现。 -HotSpot 虚拟机把它当成永久代来进行垃圾回收。但是很难确定永久代的大小，因为它受到很多因素影响，并且每次 Full GC 之后永久代的大小都会改变，所以经常会抛出 OutOfMemoryError 异常。为了更容易管理方法区，从 JDK 1.8 开始，移除永久代，并把方法区移至元空间，它位于本地内存中，而不是虚拟机内存中。 +HotSpot 虚拟机把它当成永久代来进行垃圾回收。但很难确定永久代的大小，因为它受到很多因素影响，并且每次 Full GC 之后永久代的大小都会改变，所以经常会抛出 OutOfMemoryError 异常。为了更容易管理方法区，从 JDK 1.8 开始，移除永久代，并把方法区移至元空间，它位于本地内存中，而不是虚拟机内存中。 ## 运行时常量池 运行时常量池是方法区的一部分。 -Class 文件中的常量池（编译器生成的各种字面量和符号引用）会在类加载后被放入这个区域。 +Class 文件中的常量池（编译器生成的字面量和符号引用）会在类加载后被放入这个区域。 除了在编译期生成的常量，还允许动态生成，例如 String 类的 intern()。 ## 直接内存 -在 JDK 1.4 中新加入了 NIO 类，它可以使用 Native 函数库直接分配堆外内存（Native 堆），然后通过一个存储在 Java 堆里的 DirectByteBuffer 对象作为这块内存的引用进行操作。 - -这样能在一些场景中显著提高性能，因为避免了在 Java 堆和 Native 堆中来回复制数据。 +在 JDK 1.4 中新引入了 NIO 类，它可以使用 Native 函数库直接分配堆外内存，然后通过 Java 堆里的 DirectByteBuffer 对象作为这块内存的引用进行操作。这样能在一些场景中显著提高性能，因为避免了在堆内存和堆外内存来回拷贝数据。 # 二、垃圾收集 -垃圾收集主要是针对堆和方法区进行。 - -程序计数器、虚拟机栈和本地方法栈这三个区域属于线程私有的，只存在于线程的生命周期内，线程结束之后也会消失，因此不需要对这三个区域进行垃圾回收。 +垃圾收集主要是针对堆和方法区进行。程序计数器、虚拟机栈和本地方法栈这三个区域属于线程私有的，只存在于线程的生命周期内，线程结束之后就会消失，因此不需要对这三个区域进行垃圾回收。 ## 判断一个对象是否可被回收 ### 1. 引用计数算法 -给对象添加一个引用计数器，当对象增加一个引用时计数器加 1，引用失效时计数器减 1。引用计数为 0 的对象可被回收。 +为对象添加一个引用计数器，当对象增加一个引用时计数器加 1，引用失效时计数器减 1。引用计数为 0 的对象可被回收。 -两个对象出现循环引用的情况下，此时引用计数器永远不为 0，导致无法对它们进行回收。 - -正因为循环引用的存在，因此 Java 虚拟机不使用引用计数算法。 +在两个对象出现循环引用的情况下，此时引用计数器永远不为 0，导致无法对它们进行回收。正是因为循环引用的存在，因此 Java 虚拟机不使用引用计数算法。 ```java -public class ReferenceCountingGC { +public class Test { public Object instance = null; public static void main(String[] args) { - ReferenceCountingGC objectA = new ReferenceCountingGC(); - ReferenceCountingGC objectB = new ReferenceCountingGC(); - objectA.instance = objectB; - objectB.instance = objectA; + Test a = new Test(); + Test b = new Test(); + a.instance = b; + b.instance = a; } } ``` ### 2. 可达性分析算法 -通过 GC Roots 作为起始点进行搜索，能够到达到的对象都是存活的，不可达的对象可被回收。 +以 GC Roots 为起始点进行搜索，可达的对象都是存活的，不可达的对象可被回收。 -Java 虚拟机使用该算法来判断对象是否可被回收，在 Java 中 GC Roots 一般包含以下内容： +Java 虚拟机使用该算法来判断对象是否可被回收，GC Roots 一般包含以下内容： - 虚拟机栈中局部变量表中引用的对象 - 本地方法栈中 JNI 中引用的对象 - 方法区中类静态属性引用的对象 - 方法区中的常量引用的对象 -
+
### 3. 方法区的回收 -因为方法区主要存放永久代对象，而永久代对象的回收率比新生代低很多，因此在方法区上进行回收性价比不高。 +因为方法区主要存放永久代对象，而永久代对象的回收率比新生代低很多，所以在方法区上进行回收性价比不高。 主要是对常量池的回收和对类的卸载。 -在大量使用反射、动态代理、CGLib 等 ByteCode 框架、动态生成 JSP 以及 OSGi 这类频繁自定义 ClassLoader 的场景都需要虚拟机具备类卸载功能，以保证不会出现内存溢出。 +为了避免内存溢出，在大量使用反射和动态代理的场景都需要虚拟机具备类卸载功能。 -类的卸载条件很多，需要满足以下三个条件，并且满足了也不一定会被卸载： +类的卸载条件很多，需要满足以下三个条件，并且满足了条件也不一定会被卸载： -- 该类所有的实例都已经被回收，也就是堆中不存在该类的任何实例。 +- 该类所有的实例都已经被回收，此时堆中不存在该类的任何实例。 - 加载该类的 ClassLoader 已经被回收。 - 该类对应的 Class 对象没有在任何地方被引用，也就无法在任何地方通过反射访问该类方法。 -可以通过 -Xnoclassgc 参数来控制是否对类进行卸载。 - ### 4. finalize() -finalize() 类似 C++ 的析构函数，用来做关闭外部资源等工作。但是 try-finally 等方式可以做的更好，并且该方法运行代价高昂，不确定性大，无法保证各个对象的调用顺序，因此最好不要使用。 +类似 C++ 的析构函数，用于关闭外部资源。但是 try-finally 等方式可以做得更好，并且该方法运行代价很高，不确定性大，无法保证各个对象的调用顺序，因此最好不要使用。 -当一个对象可被回收时，如果需要执行该对象的 finalize() 方法，那么就有可能在该方法中让对象重新被引用，从而实现自救。自救只能进行一次，如果回收的对象之前调用了 finalize() 方法自救，后面回收时不会调用 finalize() 方法。 +当一个对象可被回收时，如果需要执行该对象的 finalize() 方法，那么就有可能在该方法中让对象重新被引用，从而实现自救。自救只能进行一次，如果回收的对象之前调用了 finalize() 方法自救，后面回收时不会再调用该方法。 ## 引用类型 @@ -175,7 +167,7 @@ obj = null; // 使对象只被软引用关联 被弱引用关联的对象一定会被回收，也就是说它只能存活到下一次垃圾回收发生之前。 -使用 WeakReference 类来实现弱引用。 +使用 WeakReference 类来创建弱引用。 ```java Object obj = new Object(); @@ -185,11 +177,11 @@ obj = null; ### 4. 虚引用 -又称为幽灵引用或者幻影引用。一个对象是否有虚引用的存在，完全不会对其生存时间构成影响，也无法通过虚引用取得一个对象。 +又称为幽灵引用或者幻影引用，一个对象是否有虚引用的存在，不会对其生存时间造成影响，也无法通过虚引用得到一个对象。 -为一个对象设置虚引用关联的唯一目的就是能在这个对象被回收时收到一个系统通知。 +为一个对象设置虚引用的唯一目的是能在这个对象被回收时收到一个系统通知。 -使用 PhantomReference 来实现虚引用。 +使用 PhantomReference 来创建虚引用。 ```java Object obj = new Object(); @@ -201,7 +193,8 @@ obj = null; ### 1. 标记 - 清除 -
+
+ 标记要回收的对象，然后清除。 @@ -212,21 +205,23 @@ obj = null; ### 2. 标记 - 整理 -
+ +
+ 让所有存活的对象都向一端移动，然后直接清理掉端边界以外的内存。 ### 3. 复制 -
+
将内存划分为大小相等的两块，每次只使用其中一块，当这一块内存用完了就将还存活的对象复制到另一块上面，然后再把使用过的内存空间进行一次清理。 主要不足是只使用了内存的一半。 -现在的商业虚拟机都采用这种收集算法来回收新生代，但是并不是将新生代划分为大小相等的两块，而是分为一块较大的 Eden 空间和两块较小的 Survivor 空间，每次使用 Eden 空间和其中一块 Survivor。在回收时，将 Eden 和 Survivor 中还存活着的对象一次性复制到另一块 Survivor 空间上，最后清理 Eden 和使用过的那一块 Survivor。 +现在的商业虚拟机都采用这种收集算法回收新生代，但是并不是划分为大小相等的两块，而是一块较大的 Eden 空间和两块较小的 Survivor 空间，每次使用 Eden 和其中一块 Survivor。在回收时，将 Eden 和 Survivor 中还存活着的对象全部复制到另一块 Survivor 上，最后清理 Eden 和使用过的那一块 Survivor。 -HotSpot 虚拟机的 Eden 和 Survivor 的大小比例默认为 8:1，保证了内存的利用率达到 90%。如果每次回收有多于 10% 的对象存活，那么一块 Survivor 空间就不够用了，此时需要依赖于老年代进行分配担保，也就是借用老年代的空间存储放不下的对象。 +HotSpot 虚拟机的 Eden 和 Survivor 大小比例默认为 8:1，保证了内存的利用率达到 90%。如果每次回收有多于 10% 的对象存活，那么一块 Survivor 就不够用了，此时需要依赖于老年代进行空间分配担保，也就是借用老年代的空间存储放不下的对象。 ### 4. 分代收集 @@ -243,7 +238,7 @@ HotSpot 虚拟机的 Eden 和 Survivor 的大小比例默认为 8:1，保证了 以上是 HotSpot 虚拟机中的 7 个垃圾收集器，连线表示垃圾收集器可以配合使用。 -- 单线程与多线程：单线程指的是垃圾收集器只使用一个线程进行收集，而多线程使用多个线程； +- 单线程与多线程：单线程指的是垃圾收集器只使用一个线程，而多线程使用多个线程； - 串行与并行：串行指的是垃圾收集器与用户程序交替执行，这意味着在执行垃圾收集的时候需要停顿用户程序；并行指的是垃圾收集器和用户程序同时执行。除了 CMS 和 G1 之外，其它垃圾收集器都是以串行的方式执行。 ### 1. Serial 收集器 @@ -254,9 +249,9 @@ Serial 翻译为串行，也就是说它以串行的方式执行。 它是单线程的收集器，只会使用一个线程进行垃圾收集工作。 -它的优点是简单高效，对于单个 CPU 环境来说，由于没有线程交互的开销，因此拥有最高的单线程收集效率。 +它的优点是简单高效，在单个 CPU 环境下，由于没有线程交互的开销，因此拥有最高的单线程收集效率。 -它是 Client 模式下的默认新生代收集器，因为在该应用场景下，分配给虚拟机管理的内存一般来说不会很大。Serial 收集器收集几十兆甚至一两百兆的新生代停顿时间可以控制在一百多毫秒以内，只要不是太频繁，这点停顿是可以接受的。 +它是 Client 场景下的默认新生代收集器，因为在该场景下内存一般来说不会很大。它收集一两百兆垃圾的停顿时间可以控制在一百多毫秒以内，只要不是太频繁，这点停顿时间是可以接受的。 ### 2. ParNew 收集器 @@ -264,15 +259,13 @@ Serial 翻译为串行，也就是说它以串行的方式执行。 它是 Serial 收集器的多线程版本。 -是 Server 模式下的虚拟机首选新生代收集器，除了性能原因外，主要是因为除了 Serial 收集器，只有它能与 CMS 收集器配合工作。 - -默认开启的线程数量与 CPU 数量相同，可以使用 -XX:ParallelGCThreads 参数来设置线程数。 +它是 Server 场景下默认的新生代收集器，除了性能原因外，主要是因为除了 Serial 收集器，只有它能与 CMS 收集器配合使用。 ### 3. Parallel Scavenge 收集器 与 ParNew 一样是多线程收集器。 -其它收集器关注点是尽可能缩短垃圾收集时用户线程的停顿时间，而它的目标是达到一个可控制的吞吐量，它被称为“吞吐量优先”收集器。这里的吞吐量指 CPU 用于运行用户代码的时间占总时间的比值。 +其它收集器目标是尽可能缩短垃圾收集时用户线程的停顿时间，而它的目标是达到一个可控制的吞吐量，因此它被称为“吞吐量优先”收集器。这里的吞吐量指 CPU 用于运行用户程序的时间占总时间的比值。 停顿时间越短就越适合需要与用户交互的程序，良好的响应速度能提升用户体验。而高吞吐量则可以高效率地利用 CPU 时间，尽快完成程序的运算任务，适合在后台运算而不需要太多交互的任务。 @@ -284,7 +277,7 @@ Serial 翻译为串行，也就是说它以串行的方式执行。
-是 Serial 收集器的老年代版本，也是给 Client 模式下的虚拟机使用。如果用在 Server 模式下，它有两大用途： +是 Serial 收集器的老年代版本，也是给 Client 场景下的虚拟机使用。如果用在 Server 场景下，它有两大用途： - 在 JDK 1.5 以及之前版本（Parallel Old 诞生以前）中与 Parallel Scavenge 收集器搭配使用。 - 作为 CMS 收集器的后备预案，在并发收集发生 Concurrent Mode Failure 时使用。 @@ -352,9 +345,9 @@ G1 把堆划分成多个大小相等的独立区域（Region），新生代和 ## Minor GC 和 Full GC -- Minor GC：发生在新生代上，因为新生代对象存活时间很短，因此 Minor GC 会频繁执行，执行的速度一般也会比较快。 +- Minor GC：回收新生代上，因为新生代对象存活时间很短，因此 Minor GC 会频繁执行，执行的速度一般也会比较快。 -- Full GC：发生在老年代上，老年代对象其存活时间长，因此 Full GC 很少执行，执行速度会比 Minor GC 慢很多。 +- Full GC：回收老年代和新生代，老年代对象其存活时间长，因此 Full GC 很少执行，执行速度会比 Minor GC 慢很多。 ## 内存分配策略 @@ -418,11 +411,11 @@ G1 把堆划分成多个大小相等的独立区域（Region），新生代和 # 四、类加载机制 -类是在运行期间第一次使用时动态加载的，而不是编译时期一次性加载。因为如果在编译时期一次性加载，那么会占用很多的内存。 +类是在运行期间第一次使用时动态加载的，而不是一次性加载。因为如果一次性加载，那么会占用很多的内存。 ## 类的生命周期 -
+
包括以下 7 个阶段： @@ -444,9 +437,10 @@ G1 把堆划分成多个大小相等的独立区域（Region），新生代和 加载过程完成以下三件事： -- 通过一个类的全限定名来获取定义此类的二进制字节流。 -- 将这个字节流所代表的静态存储结构转化为方法区的运行时存储结构。 -- 在内存中生成一个代表这个类的 Class 对象，作为方法区这个类的各种数据的访问入口。 +- 通过类的完全限定名称获取定义该类的二进制字节流。 +- 将该字节流表示的静态存储结构转换为方法区的运行时存储结构。 +- 在内存中生成一个代表该类的 Class 对象，作为方法区中该类各种数据的访问入口。 + 其中二进制字节流可以从以下方式中获取： @@ -463,9 +457,7 @@ G1 把堆划分成多个大小相等的独立区域（Region），新生代和 类变量是被 static 修饰的变量，准备阶段为类变量分配内存并设置初始值，使用的是方法区的内存。 -实例变量不会在这阶段分配内存，它将会在对象实例化时随着对象一起分配在堆中。 - -注意，实例化不是类加载的一个过程，类加载发生在所有实例化操作之前，并且类加载只进行一次，实例化可以进行多次。 +实例变量不会在这阶段分配内存，它会在对象实例化时随着对象一起被分配在堆中。应该注意到，实例化不是类加载的一个过程，类加载发生在所有实例化操作之前，并且类加载只进行一次，实例化可以进行多次。 初始值一般为 0 值，例如下面的类变量 value 被初始化为 0 而不是 123。 @@ -473,7 +465,7 @@ G1 把堆划分成多个大小相等的独立区域（Region），新生代和 public static int value = 123; ``` -如果类变量是常量，那么会按照表达式来进行初始化，而不是赋值为 0。 +如果类变量是常量，那么它将初始化为表达式所定义的值而不是 0。例如下面的常量 value 被初始化为 123 而不是 0。 ```java public static final int value = 123; @@ -485,15 +477,17 @@ public static final int value = 123; 其中解析过程在某些情况下可以在初始化阶段之后再开始，这是为了支持 Java 的动态绑定。 +
+ ### 5. 初始化 -初始化阶段才真正开始执行类中定义的 Java 程序代码。初始化阶段即虚拟机执行类构造器 <clinit>() 方法的过程。 +
-在准备阶段，类变量已经赋过一次系统要求的初始值，而在初始化阶段，根据程序员通过程序制定的主观计划去初始化类变量和其它资源。 +初始化阶段才真正开始执行类中定义的 Java 程序代码。初始化阶段是虚拟机执行类构造器 <clinit>() 方法的过程。在准备阶段，类变量已经赋过一次系统要求的初始值，而在初始化阶段，根据程序员通过程序制定的主观计划去初始化类变量和其它资源。 -<clinit>() 方法具有以下特点： +在准备阶段，已经为类变量分配了系统所需的初始值，并且在初始化阶段，根据程序员通过程序进行的主观计划来初始化类变量和其他资源。 -- 是由编译器自动收集类中所有类变量的赋值动作和静态语句块中的语句合并产生的，编译器收集的顺序由语句在源文件中出现的顺序决定。特别注意的是，静态语句块只能访问到定义在它之前的类变量，定义在它之后的类变量只能赋值，不能访问。例如以下代码： +<clinit>() 是由编译器自动收集类中所有类变量的赋值动作和静态语句块中的语句合并产生的，编译器收集的顺序由语句在源文件中出现的顺序决定。特别注意的是，静态语句块只能访问到定义在它之前的类变量，定义在它之后的类变量只能赋值，不能访问。例如以下代码： ```java public class Test { @@ -505,9 +499,7 @@ public class Test { } ``` -- 与类的构造函数（或者说实例构造器 <init>()）不同，不需要显式的调用父类的构造器。虚拟机会自动保证在子类的 <clinit>() 方法运行之前，父类的 <clinit>() 方法已经执行结束。因此虚拟机中第一个执行 <clinit>() 方法的类肯定为 java.lang.Object。 - -- 由于父类的 <clinit>() 方法先执行，也就意味着父类中定义的静态语句块的执行要优先于子类。例如以下代码： +由于父类的 <clinit>() 方法先执行，也就意味着父类中定义的静态语句块的执行要优先于子类。例如以下代码： ```java static class Parent { @@ -526,11 +518,9 @@ public static void main(String[] args) { } ``` -- <clinit>() 方法对于类或接口不是必须的，如果一个类中不包含静态语句块，也没有对类变量的赋值操作，编译器可以不为该类生成 <clinit>() 方法。 - -- 接口中不可以使用静态语句块，但仍然有类变量初始化的赋值操作，因此接口与类一样都会生成 <clinit>() 方法。但接口与类不同的是，执行接口的 <clinit>() 方法不需要先执行父接口的 <clinit>() 方法。只有当父接口中定义的变量使用时，父接口才会初始化。另外，接口的实现类在初始化时也一样不会执行接口的 <clinit>() 方法。 +接口中不可以使用静态语句块，但仍然有类变量初始化的赋值操作，因此接口与类一样都会生成 <clinit>() 方法。但接口与类不同的是，执行接口的 <clinit>() 方法不需要先执行父接口的 <clinit>() 方法。只有当父接口中定义的变量使用时，父接口才会初始化。另外，接口的实现类在初始化时也一样不会执行接口的 <clinit>() 方法。 -- 虚拟机会保证一个类的 <clinit>() 方法在多线程环境下被正确的加锁和同步，如果多个线程同时初始化一个类，只会有一个线程执行这个类的 <clinit>() 方法，其它线程都会阻塞等待，直到活动线程执行 <clinit>() 方法完毕。如果在一个类的 <clinit>() 方法中有耗时的操作，就可能造成多个线程阻塞，在实际过程中此种阻塞很隐蔽。 +虚拟机会保证一个类的 <clinit>() 方法在多线程环境下被正确的加锁和同步，如果多个线程同时初始化一个类，只会有一个线程执行这个类的 <clinit>() 方法，其它线程都会阻塞等待，直到活动线程执行 <clinit>() 方法完毕。如果在一个类的 <clinit>() 方法中有耗时的操作，就可能造成多个线程阻塞，在实际过程中此种阻塞很隐蔽。 ## 类初始化时机 @@ -572,7 +562,7 @@ System.out.println(ConstClass.HELLOWORLD); ## 类与类加载器 -两个类相等需要类本身相等，并且使用同一个类加载器进行加载。这是因为每一个类加载器都拥有一个独立的类名称空间。 +两个类相等，需要类本身相等，并且使用同一个类加载器进行加载。这是因为每一个类加载器都拥有一个独立的类名称空间。 这里的相等，包括类的 Class 对象的 equals() 方法、isAssignableFrom() 方法、isInstance() 方法的返回结果为 true，也包括使用 instanceof 关键字做对象所属关系判定结果为 true。 @@ -580,9 +570,9 @@ System.out.println(ConstClass.HELLOWORLD); 从 Java 虚拟机的角度来讲，只存在以下两种不同的类加载器： -- 启动类加载器（Bootstrap ClassLoader），这个类加载器用 C++ 实现，是虚拟机自身的一部分； +- 启动类加载器（Bootstrap ClassLoader），使用 C++ 实现，是虚拟机自身的一部分； -- 所有其他类的加载器，这些类由 Java 实现，独立于虚拟机外部，并且全都继承自抽象类 java.lang.ClassLoader。 +- 所有其它类的加载器，使用 Java 实现，独立于虚拟机，继承自抽象类 java.lang.ClassLoader。 从 Java 开发人员的角度看，类加载器可以划分得更细致一些： @@ -592,23 +582,25 @@ System.out.println(ConstClass.HELLOWORLD); - 应用程序类加载器（Application ClassLoader）这个类加载器是由 AppClassLoader（sun.misc.Launcher$AppClassLoader）实现的。由于这个类加载器是 ClassLoader 中的 getSystemClassLoader() 方法的返回值，因此一般称为系统类加载器。它负责加载用户类路径（ClassPath）上所指定的类库，开发者可以直接使用这个类加载器，如果应用程序中没有自定义过自己的类加载器，一般情况下这个就是程序中默认的类加载器。 +
+ ## 双亲委派模型 -应用程序都是由三种类加载器相互配合进行加载的，如果有必要，还可以加入自己定义的类加载器。 +应用程序是由三种类加载器互相配合从而实现类加载，除此之外还可以加入自己定义的类加载器。 -下图展示的类加载器之间的层次关系，称为类加载器的双亲委派模型（Parents Delegation Model）。该模型要求除了顶层的启动类加载器外，其余的类加载器都应有自己的父类加载器。这里类加载器之间的父子关系一般通过组合（Composition）关系来实现，而不是通过继承（Inheritance）的关系实现。 +下图展示了类加载器之间的层次关系，称为双亲委派模型（Parents Delegation Model）。该模型要求除了顶层的启动类加载器外，其它的类加载器都要有自己的父类加载器。类加载器之间的父子关系一般通过组合关系（Composition）来实现，而不是继承关系（Inheritance）。 -
+
### 1. 工作过程 -一个类加载器首先将类加载请求传送到父类加载器，只有当父类加载器无法完成类加载请求时才尝试加载。 +一个类加载器首先将类加载请求转发到父类加载器，只有当父类加载器无法完成时才尝试自己加载。 ### 2. 好处 使得 Java 类随着它的类加载器一起具有一种带有优先级的层次关系，从而使得基础类得到统一。 -例如 java.lang.Object 存放在 rt.jar 中，如果编写另外一个 java.lang.Object 的类并放到 ClassPath 中，程序可以编译通过。由于双亲委派模型的存在，所以在 rt.jar 中的 Object 比在 ClassPath 中的 Object 优先级更高，这是因为 rt.jar 中的 Object 使用的是启动类加载器，而 ClassPath 中的 Object 使用的是应用程序类加载器。rt.jar 中的 Object 优先级更高，那么程序中所有的 Object 都是这个 Object。 +例如 java.lang.Object 存放在 rt.jar 中，如果编写另外一个 java.lang.Object 并放到 ClassPath 中，程序可以编译通过。由于双亲委派模型的存在，所以在 rt.jar 中的 Object 比在 ClassPath 中的 Object 优先级更高，这是因为 rt.jar 中的 Object 使用的是启动类加载器，而 ClassPath 中的 Object 使用的是应用程序类加载器。rt.jar 中的 Object 优先级更高，那么程序中所有的 Object 都是这个 Object。 ### 3. 实现 @@ -662,7 +654,7 @@ public abstract class ClassLoader { FileSystemClassLoader 是自定义类加载器，继承自 java.lang.ClassLoader，用于加载文件系统上的类。它首先根据类的全名在文件系统上查找类的字节代码文件（.class 文件），然后读取该文件内容，最后通过 defineClass() 方法来把这些字节代码转换成 java.lang.Class 类的实例。 -java.lang.ClassLoader 的 loadClass() 实现了双亲委派模型的逻辑，因此自定义类加载器一般不去重写它，但是需要重写 findClass() 方法。 +java.lang.ClassLoader 的 loadClass() 实现了双亲委派模型的逻辑，自定义类加载器一般不去重写它，但是需要重写 findClass() 方法。 ```java public class FileSystemClassLoader extends ClassLoader { diff --git "a/convert/Leetcode \351\242\230\350\247\243.md" "b/convert/Leetcode \351\242\230\350\247\243.md" index 7c7cce5..9857154 100644 --- "a/convert/Leetcode \351\242\230\350\247\243.md" +++ "b/convert/Leetcode \351\242\230\350\247\243.md" @@ -207,7 +207,7 @@ Output: "apple" ``` -题目描述：删除 s 中的一些字符，使得它构成字符串列表 d 中的一个字符串，找出能构成的最长字符串。如果有多个相同长度的结果，返回字典序的最大字符串。 +题目描述：删除 s 中的一些字符，使得它构成字符串列表 d 中的一个字符串，找出能构成的最长字符串。如果有多个相同长度的结果，返回字典序的最小字符串。 ```java public String findLongestWord(String s, List d) { @@ -353,8 +353,10 @@ public List topKFrequent(int[] nums, int k) { } List topK = new ArrayList<>(); for (int i = buckets.length - 1; i >= 0 && topK.size() < k; i--) { - if (buckets[i] != null) { + if (buckets[i].size() <= (k - topK.size())) { topK.addAll(buckets[i]); + } else { + topK.addAll(buckets[i].subList(0, k - topK.size())); } } return topK; @@ -2266,7 +2268,7 @@ public void solveSudoku(char[][] board) { colsUsed[j][num] = true; cubesUsed[cubeNum(i, j)][num] = true; } - backtracking(i, 0); + backtracking(0, 0); } private boolean backtracking(int row, int col) { @@ -2380,7 +2382,9 @@ private void backtracking(int row) { 第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达，走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。 -
$dp[i]=dp[i-1]+dp[i-2]$

+$$ +dp[i]=dp[i-1]+dp[i-2] +$$ 考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关，因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2]，使得原来的 O(N) 空间复杂度优化为 O(1) 复杂度。 @@ -2409,7 +2413,9 @@ public int climbStairs(int n) { 由于不能抢劫邻近住户，如果抢劫了第 i -1 个住户，那么就不能再抢劫第 i 个住户，所以 -
$dp[i]=max(dp[i-2]+nums[i],dp[i-1])$

+$$ +dp[i]=max(dp[i-2]+nums[i],dp[i-1]) +$$ ```java public int rob(int[] nums) { @@ -2461,7 +2467,9 @@ private int rob(int[] nums, int first, int last) { 综上所述，错误装信数量方式数量为： -
$dp[i]=(i-1)*dp[i-2]+(i-1)*dp[i-1]$

+$$ +dp[i]=(i-1)*dp[i-2]+(i-1)*dp[i-1] +$$ **母牛生产** @@ -2471,7 +2479,9 @@ private int rob(int[] nums, int first, int last) { 第 i 年成熟的牛的数量为： -
$dp[i]=dp[i-1]+dp[i-3]$

+$$ +dp[i]=dp[i-1]+dp[i-3] +$$ ### 矩阵路径 @@ -2712,7 +2722,9 @@ public int numDecodings(String s) { 因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列，此时 {Sn} 就构成了递增子序列，需要对前面的求解方程做修改，令 dp[n] 最小为 1，即： -
$dp[n]=max\{1,dp[i]+1|S_i
+$$ +dp[n]=max\{1,dp[i]+1|S_iN 为结尾，因此 dp[N] 不是序列的最长递增子序列的长度，需要遍历 dp 数组找出最大值才是所要的结果，max{ dp[i] | 1 <= i <= N} 即为所求。 @@ -2877,7 +2889,9 @@ public int wiggleMaxLength(int[] nums) { 综上，最长公共子序列的状态转移方程为： -
$dp[i][j]=\left\{\begin{array}{rcl}dp[i-1][j-1]&&{S1_i==S2_j}\\max(dp[i-1][j],dp[i][j-1])&&{S1_i<>S2_j}\end{array}\right.$

+$$ +dp[i][j]=\left\{\begin{array}{rcl}dp[i-1][j-1]&&{S1_i==S2_j}\\max(dp[i-1][j],dp[i][j-1])&&{S1_i<>S2_j}\end{array}\right. +$$ 对于长度为 N 的序列 S1 和长度为 M 的序列 S2，dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。 @@ -2915,7 +2929,9 @@ public int lengthOfLCS(int[] nums1, int[] nums2) { 第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。因此，0-1 背包的状态转移方程为： -
$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+v)$

+$$ +dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+v) +$$ ```java public int knapsack(int W, int N, int[] weights, int[] values) { @@ -2938,7 +2954,9 @@ public int knapsack(int W, int N, int[] weights, int[] values) { 在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道，前 i 件物品的状态仅与前 i-1 件物品的状态有关，因此可以将 dp 定义为一维数组，其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时， -
$dp[j]=max(dp[j],dp[j-w]+v)$

+$$ +dp[j]=max(dp[j],dp[j-w]+v) +$$ 因为 dp[j-w] 表示 dp[i-1][j-w]，因此不能先求 dp[i][j-w]，以防将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w]，在程序实现时需要按倒序来循环求解。 @@ -3000,7 +3018,6 @@ public boolean canPartition(int[] nums) { int W = sum / 2; boolean[] dp = new boolean[W + 1]; dp[0] = true; - Arrays.sort(nums); for (int num : nums) { // 0-1 背包一个物品只能用一次 for (int i = W; i >= num; i--) { // 从后往前，先计算 dp[i] 再计算 dp[i-num] dp[i] = dp[i] || dp[i - num]; @@ -5645,7 +5662,7 @@ Output: 5 Explanation: The longest harmonious subsequence is [3,2,2,2,3]. ``` -和谐序列中最大数和最小数只差正好为 1，应该注意的是序列的元素不一定是数组的连续元素。 +和谐序列中最大数和最小数之差正好为 1，应该注意的是序列的元素不一定是数组的连续元素。 ```java public int findLHS(int[] nums) { diff --git "a/convert/Leetcode-Database \351\242\230\350\247\243.md" "b/convert/Leetcode-Database \351\242\230\350\247\243.md" index e43de6b..2838dc3 100644 --- "a/convert/Leetcode-Database \351\242\230\350\247\243.md" +++ "b/convert/Leetcode-Database \351\242\230\350\247\243.md" @@ -483,7 +483,7 @@ https://leetcode.com/problems/customers-who-never-order/description/ ## Description -Curstomers 表： +Customers 表： ```html +----+-------+ diff --git a/convert/MySQL.md b/convert/MySQL.md index 59d2c3f..8599c12 100644 --- a/convert/MySQL.md +++ b/convert/MySQL.md @@ -16,7 +16,7 @@ B+ Tree 是基于 B Tree 和叶子节点顺序访问指针进行实现，它具 在 B+ Tree 中，一个节点中的 key 从左到右非递减排列，如果某个指针的左右相邻 key 分别是 keyi 和 keyi+1，且不为 null，则该指针指向节点的所有 key 大于等于 keyi 且小于等于 keyi+1。 -
+
### 2. 操作 @@ -58,11 +58,11 @@ B+ Tree 是基于 B Tree 和叶子节点顺序访问指针进行实现，它具 InnoDB 的 B+Tree 索引分为主索引和辅助索引。主索引的叶子节点 data 域记录着完整的数据记录，这种索引方式被称为聚簇索引。因为无法把数据行存放在两个不同的地方，所以一个表只能有一个聚簇索引。 -
+
辅助索引的叶子节点的 data 域记录着主键的值，因此在使用辅助索引进行查找时，需要先查找到主键值，然后再到主索引中进行查找。 -
+
### 2. 哈希索引 diff --git a/convert/Socket.md b/convert/Socket.md index 82d7626..6365b9c 100644 --- a/convert/Socket.md +++ b/convert/Socket.md @@ -23,11 +23,11 @@ Unix 有五种 I/O 模型： ## 阻塞式 I/O -应用进程被阻塞，直到数据复制到应用进程缓冲区中才返回。 +应用进程被阻塞，直到数据从内核缓冲区复制到应用进程缓冲区中才返回。 -应该注意到，在阻塞的过程中，其它程序还可以执行，因此阻塞不意味着整个操作系统都被阻塞。因为其他程序还可以执行，所以不消耗 CPU 时间，这种模型的 CPU 利用率效率会比较高。 +应该注意到，在阻塞的过程中，其它应用进程还可以执行，因此阻塞不意味着整个操作系统都被阻塞。因为其它应用进程还可以执行，所以不消耗 CPU 时间，这种模型的 CPU 利用率效率会比较高。 -下图中，recvfrom 用于接收 Socket 传来的数据，并复制到应用进程的缓冲区 buf 中。这里把 recvfrom() 当成系统调用。 +下图中，recvfrom() 用于接收 Socket 传来的数据，并复制到应用进程的缓冲区 buf 中。这里把 recvfrom() 当成系统调用。 ```c ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_addr, socklen_t *addrlen); @@ -39,7 +39,7 @@ ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr * 应用进程执行系统调用之后，内核返回一个错误码。应用进程可以继续执行，但是需要不断的执行系统调用来获知 I/O 是否完成，这种方式称为轮询（polling）。 -由于 CPU 要处理更多的系统调用，因此这种模型的 CPU 利用率是比较低的。 +由于 CPU 要处理更多的系统调用，因此这种模型的 CPU 利用率比较低。
diff --git "a/convert/\344\273\243\347\240\201\345\217\257\350\257\273\346\200\247.md" "b/convert/\344\273\243\347\240\201\345\217\257\350\257\273\346\200\247.md" index f41fa23..2d3b702 100644 --- "a/convert/\344\273\243\347\240\201\345\217\257\350\257\273\346\200\247.md" +++ "b/convert/\344\273\243\347\240\201\345\217\257\350\257\273\346\200\247.md" @@ -35,9 +35,12 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF - 用 min、max 表示数量范围； - 用 first、last 表示访问空间的包含范围； + +
+ - begin、end 表示访问空间的排除范围，即 end 不包含尾部。 -
+
# 四、良好的代码风格 diff --git "a/convert/\345\210\206\345\270\203\345\274\217.md" "b/convert/\345\210\206\345\270\203\345\274\217.md" index 6469883..f86f884 100644 --- "a/convert/\345\210\206\345\270\203\345\274\217.md" +++ "b/convert/\345\210\206\345\270\203\345\274\217.md" @@ -47,7 +47,7 @@ EXPIRE 指令可以为一个键值对设置一个过期时间，从而避免了 Zookeeper 提供了一种树形结构级的命名空间，/app1/p_1 节点的父节点为 /app1。 -
+
### 2. 节点类型 @@ -88,7 +88,7 @@ Zookeeper 提供了一种树形结构级的命名空间，/app1/p_1 节点的父 2. 之后将本地消息表中的消息转发到 Kafka 等消息队列中，如果转发成功则将消息从本地消息表中删除，否则继续重新转发。 3. 在分布式事务操作的另一方从消息队列中读取一个消息，并执行消息中的操作。 -
+
## 2PC @@ -100,7 +100,7 @@ Zookeeper 提供了一种树形结构级的命名空间，/app1/p_1 节点的父 协调者询问参与者事务是否执行成功，参与者发回事务执行结果。 -
+
#### 1.2 提交阶段 @@ -108,7 +108,7 @@ Zookeeper 提供了一种树形结构级的命名空间，/app1/p_1 节点的父 需要注意的是，在准备阶段，参与者执行了事务，但是还未提交。只有在提交阶段接收到协调者发来的通知后，才进行提交或者回滚。 -
+
### 2. 存在的问题 @@ -132,7 +132,7 @@ Zookeeper 提供了一种树形结构级的命名空间，/app1/p_1 节点的父 分布式系统不可能同时满足一致性（C：Consistency）、可用性（A：Availability）和分区容忍性（P：Partition Tolerance），最多只能同时满足其中两项。 -
+
## 一致性 @@ -169,7 +169,6 @@ BASE 是基本可用（Basically Available）、软状态（Soft State）和最 BASE 理论是对 CAP 中一致性和可用性权衡的结果，它的核心思想是：即使无法做到强一致性，但每个应用都可以根据自身业务特点，采用适当的方式来使系统达到最终一致性。 -
## 基本可用 @@ -291,19 +290,19 @@ Raft 也是分布式一致性协议，主要是用来竞选主节点。 - 来自客户端的修改都会被传入 Leader。注意该修改还未被提交，只是写入日志中。 -
+
- Leader 会把修改复制到所有 Follower。 -
+
- Leader 会等待大多数的 Follower 也进行了修改，然后才将修改提交。 -
+
- 此时 Leader 会通知的所有 Follower 让它们也提交修改，此时所有节点的值达成一致。 -
+
# 参考 diff --git "a/convert/\345\211\221\346\214\207 offer \351\242\230\350\247\243.md" "b/convert/\345\211\221\346\214\207 offer \351\242\230\350\247\243.md" index 1bf9744..d68fd12 100644 --- "a/convert/\345\211\221\346\214\207 offer \351\242\230\350\247\243.md" +++ "b/convert/\345\211\221\346\214\207 offer \351\242\230\350\247\243.md" @@ -4,16 +4,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF -# 1. 前言 - -本文的绘图可通过以下途径免费获得并使用： - -- [ProcessOn](https://www.processon.com/view/5a3e4c7be4b0909c1aa18b49) -- [DrawIO](https://drive.google.com/file/d/1nSSCpPUC05MFoeFuf_aeTtkm7dG5-bJ1/view?usp=sharing) - -# 2. 实现 Singleton - -[单例模式](设计模式.md) +部分绘图文件可以在这里免费下载：[剑指 Offer](https://www.processon.com/view/5a3e4c7be4b0909c1aa18b49)，后续会慢慢把所有题目都配上 GIF 演示图。 # 3. 数组中重复的数字 @@ -33,24 +24,13 @@ Output: ## 解题思路 -要求复杂度为 O(N) + O(1)，也就是时间复杂度 O(N)，空间复杂度 O(1)。因此不能使用排序的方法，也不能使用额外的标记数组。牛客网讨论区这一题的首票答案使用 nums[i] + length 来将元素标记，这么做会有加法溢出问题。 +要求是时间复杂度 O(N)，空间复杂度 O(1)。因此不能使用排序的方法，也不能使用额外的标记数组。 -这种数组元素在 [0, n-1] 范围内的问题，可以将值为 i 的元素调整到第 i 个位置上。 +对于这种数组元素在 [0, n-1] 范围内的问题，可以将值为 i 的元素调整到第 i 个位置上进行求解。 -以 (2, 3, 1, 0, 2, 5) 为例： - -```text -position-0 : (2,3,1,0,2,5) // 2 <-> 1 - (1,3,2,0,2,5) // 1 <-> 3 - (3,1,2,0,2,5) // 3 <-> 0 - (0,1,2,3,2,5) // already in position -position-1 : (0,1,2,3,2,5) // already in position -position-2 : (0,1,2,3,2,5) // already in position -position-3 : (0,1,2,3,2,5) // already in position -position-4 : (0,1,2,3,2,5) // nums[i] == nums[nums[i]], exit -``` +以 (2, 3, 1, 0, 2, 5) 为例，遍历到位置 4 时，该位置上的数为 2，但是第 2 个位置上已经有一个 2 的值了，因此可以知道 2 重复： -遍历到位置 4 时，该位置上的数为 2，但是第 2 个位置上已经有一个 2 的值了，因此可以知道 2 重复。 +
```java public boolean duplicate(int[] nums, int length, int[] duplication) { @@ -81,7 +61,7 @@ private void swap(int[] nums, int i, int j) { ## 题目描述 -在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。 +给定一个二维数组，其每一行从左到右递增排序，从上到下也是递增排序。给定一个数，判断这个数是否在该二维数组中。 ```html Consider the following matrix: @@ -99,13 +79,11 @@ Given target = 20, return false. ## 解题思路 -从右上角开始查找。矩阵中的一个数，它左边的数都比它小，下边的数都比它大。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间。 +要求时间复杂度 O(M + N)，空间复杂度 O(1)。 -复杂度：O(M + N) + O(1) +该二维数组中的一个数，它左边的数都比它小，下边的数都比它大。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。 -当前元素的查找区间为左下角的所有元素，例如元素 12 的查找区间如下： - -
+
```java public boolean Find(int target, int[][] matrix) { @@ -136,10 +114,10 @@ public boolean Find(int target, int[][] matrix) { ```text Input: -"We Are Happy" +"A B" Output: -"We%20Are%20Happy" +"A%20B" ``` ## 解题思路 @@ -150,6 +128,8 @@ Output: 从后向前遍是为了在改变 P2 所指向的内容时，不会影响到 P1 遍历原来字符串的内容。 +
+ ```java public String replaceSpace(StringBuffer str) { int P1 = str.length() - 1; @@ -178,30 +158,16 @@ public String replaceSpace(StringBuffer str) { ## 题目描述 -输入链表的第一个节点，从尾到头反过来打印出每个结点的值。 +从尾到头反过来打印出每个结点的值。 -
+
## 解题思路 -### 使用栈 - -```java -public ArrayList printListFromTailToHead(ListNode listNode) { - Stack stack = new Stack<>(); - while (listNode != null) { - stack.add(listNode.val); - listNode = listNode.next; - } - ArrayList ret = new ArrayList<>(); - while (!stack.isEmpty()) - ret.add(stack.pop()); - return ret; -} -``` - ### 使用递归 +
+ ```java public ArrayList printListFromTailToHead(ListNode listNode) { ArrayList ret = new ArrayList<>(); @@ -222,6 +188,8 @@ public ArrayList printListFromTailToHead(ListNode listNode) { - 头结点是在头插法中使用的一个额外节点，这个节点不存储值； - 第一个节点就是链表的第一个真正存储值的节点。 +
+ ```java public ArrayList printListFromTailToHead(ListNode listNode) { // 头插法构建逆序链表 @@ -243,16 +211,20 @@ public ArrayList printListFromTailToHead(ListNode listNode) { } ``` -### 使用 Collections.reverse() +### 使用栈 + +
```java public ArrayList printListFromTailToHead(ListNode listNode) { - ArrayList ret = new ArrayList<>(); + Stack stack = new Stack<>(); while (listNode != null) { - ret.add(listNode.val); + stack.add(listNode.val); listNode = listNode.next; } - Collections.reverse(ret); + ArrayList ret = new ArrayList<>(); + while (!stack.isEmpty()) + ret.add(stack.pop()); return ret; } ``` @@ -270,12 +242,14 @@ preorder = [3,9,20,15,7] inorder = [9,3,15,20,7] ``` -
+
## 解题思路 前序遍历的第一个值为根节点的值，使用这个值将中序遍历结果分成两部分，左部分为树的左子树中序遍历结果，右部分为树的右子树中序遍历的结果。 +
+ ```java // 缓存中序遍历数组每个值对应的索引 private Map indexForInOrders = new HashMap<>(); @@ -324,11 +298,11 @@ public class TreeLinkNode { ① 如果一个节点的右子树不为空，那么该节点的下一个节点是右子树的最左节点； -
+
② 否则，向上找第一个左链接指向的树包含该节点的祖先节点。 -
+
```java public TreeLinkNode GetNext(TreeLinkNode pNode) { @@ -361,7 +335,8 @@ public TreeLinkNode GetNext(TreeLinkNode pNode) { in 栈用来处理入栈（push）操作，out 栈用来处理出栈（pop）操作。一个元素进入 in 栈之后，出栈的顺序被反转。当元素要出栈时，需要先进入 out 栈，此时元素出栈顺序再一次被反转，因此出栈顺序就和最开始入栈顺序是相同的，先进入的元素先退出，这就是队列的顺序。 -
+
+ ```java Stack in = new Stack(); @@ -391,13 +366,16 @@ public int pop() throws Exception { 求斐波那契数列的第 n 项，n <= 39。 -
$f(n)=\left\{\begin{array}{rcl}0&&{n=0}\\1&&{n=1}\\f(n-1)+f(n-2)&&{n>1}\end{array}\right.$

+$$ +f(n)=\left\{\begin{array}{rcl}0&&{n=0}\\1&&{n=1}\\f(n-1)+f(n-2)&&{n>1}\end{array}\right. +$$ ## 解题思路 如果使用递归求解，会重复计算一些子问题。例如，计算 f(10) 需要计算 f(9) 和 f(8)，计算 f(9) 需要计算 f(8) 和 f(7)，可以看到 f(8) 被重复计算了。 -
+
+ 递归是将一个问题划分成多个子问题求解，动态规划也是如此，但是动态规划会把子问题的解缓存起来，从而避免重复求解子问题。 @@ -458,6 +436,8 @@ public class Solution { 一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 +
+ ## 解题思路 ```java @@ -483,6 +463,8 @@ public int JumpFloor(int n) { 我们可以用 2\*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2\*1 的小矩形无重叠地覆盖一个 2\*n 的大矩形，总共有多少种方法？ +
+ ## 解题思路 ```java @@ -508,6 +490,8 @@ public int RectCover(int n) { 一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级... 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 +
+ ## 解题思路 ### 动态规划 @@ -630,7 +614,7 @@ private int minNumber(int[] nums, int l, int h) { 例如下面的矩阵包含了一条 bfce 路径。 -
+
## 解题思路 @@ -838,7 +822,9 @@ public int NumberOf1(int n) { 下面的讨论中 x 代表 base，n 代表 exponent。 -
$x^n=\left\{\begin{array}{rcl}(x*x)^{n/2}&&{n\%2=0}\\x*(x*x)^{n/2}&&{n\%2=1}\end{array}\right.$

+$$ +x^n=\left\{\begin{array}{rcl}(x*x)^{n/2}&&{n\%2=0}\\x*(x*x)^{n/2}&&{n\%2=1}\end{array}\right. +$$ 因为 (x\*x)n/2 可以通过递归求解，并且每次递归 n 都减小一半，因此整个算法的时间复杂度为 O(logN)。 @@ -909,6 +895,8 @@ private void printNumber(char[] number) {
+② 如果链表只有一个节点，那么直接 + ② 否则，就需要先遍历链表，找到节点的前一个节点，然后让前一个节点指向 null，时间复杂度为 O(N)。
@@ -925,10 +913,15 @@ public ListNode deleteNode(ListNode head, ListNode tobeDelete) { tobeDelete.val = next.val; tobeDelete.next = next.next; } else { - ListNode cur = head; - while (cur.next != tobeDelete) - cur = cur.next; - cur.next = null; + if (head == tobeDelete) + // 只有一个节点 + head = null; + else { + ListNode cur = head; + while (cur.next != tobeDelete) + cur = cur.next; + cur.next = null; + } } return head; } @@ -1057,6 +1050,8 @@ public boolean isNumeric(char[] str) { 需要保证奇数和奇数，偶数和偶数之间的相对位置不变，这和书本不太一样。 +
+ ## 解题思路 ```java @@ -1115,11 +1110,12 @@ public ListNode FindKthToTail(ListNode head, int k) { ## 解题思路 -使用双指针，一个指针 fast 每次移动两个节点，一个指针 slow 每次移动一个节点。因为存在环，所以两个指针必定相遇在环中的某个节点上。假设相遇点在下图的 y6 位置，此时 fast 移动的节点数为 x+2y+z，slow 为 x+y，由于 fast 速度比 slow 快一倍，因此 x+2y+z=2(x+y)，得到 x=z。 +使用双指针，一个指针 fast 每次移动两个节点，一个指针 slow 每次移动一个节点。因为存在环，所以两个指针必定相遇在环中的某个节点上。假设相遇点在下图的 z1 位置，此时 fast 移动的节点数为 x+2y+z，slow 为 x+y，由于 fast 速度比 slow 快一倍，因此 x+2y+z=2(x+y)，得到 x=z。 在相遇点，slow 要到环的入口点还需要移动 z 个节点，如果让 fast 重新从头开始移动，并且速度变为每次移动一个节点，那么它到环入口点还需要移动 x 个节点。在上面已经推导出 x=z，因此 fast 和 slow 将在环入口点相遇。 -
+
+ ```java public ListNode EntryNodeOfLoop(ListNode pHead) { @@ -1316,7 +1312,7 @@ boolean isSymmetrical(TreeNode t1, TreeNode t2) { 下图的矩阵顺时针打印结果为：1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10 -
+
## 解题思路 @@ -2666,6 +2662,8 @@ public ArrayList maxInWindows(int[] num, int size) { 把 n 个骰子仍在地上，求点数和为 s 的概率。 +
+ ## 解题思路 ### 动态规划解法 @@ -2737,6 +2735,8 @@ public List> dicesSum(int n) { 五张牌，其中大小鬼为癞子，牌面大小为 0。判断这五张牌是否能组成顺子。 +
+ ## 解题思路 ```java @@ -2794,6 +2794,8 @@ public int LastRemaining_Solution(int n, int m) { 可以有一次买入和一次卖出，那么买入必须在前。求最大收益。 +
+ ## 解题思路 使用贪心策略，假设第 i 轮进行卖出操作，买入操作价格应该在 i 之前并且价格最低。 @@ -2864,6 +2866,8 @@ public int Add(int a, int b) { 给定一个数组 A[0, 1,..., n-1]，请构建一个数组 B[0, 1,..., n-1]，其中 B 中的元素 B[i]=A[0]\*A[1]\*...\*A[i-1]\*A[i+1]\*...\*A[n-1]。要求不能使用除法。 +
+ ## 解题思路 ```java diff --git "a/convert/\346\225\260\346\215\256\345\272\223\347\263\273\347\273\237\345\216\237\347\220\206.md" "b/convert/\346\225\260\346\215\256\345\272\223\347\263\273\347\273\237\345\216\237\347\220\206.md" index 9a3ac0c..5dd117c 100644 --- "a/convert/\346\225\260\346\215\256\345\272\223\347\263\273\347\273\237\345\216\237\347\220\206.md" +++ "b/convert/\346\225\260\346\215\256\345\272\223\347\263\273\347\273\237\345\216\237\347\220\206.md" @@ -10,7 +10,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 事务指的是满足 ACID 特性的一组操作，可以通过 Commit 提交一个事务，也可以使用 Rollback 进行回滚。 -
+
## ACID @@ -43,7 +43,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF - 在并发的情况下，多个事务并行执行，事务不仅要满足原子性，还需要满足隔离性，才能满足一致性。 - 事务满足持久化是为了能应对数据库崩溃的情况。 -
+
## AUTOCOMMIT @@ -57,26 +57,26 @@ MySQL 默认采用自动提交模式。也就是说，如果不显式使用`STAR T1 和 T2 两个事务都对一个数据进行修改，T1 先修改，T2 随后修改，T2 的修改覆盖了 T1 的修改。 -
+
## 读脏数据 T1 修改一个数据，T2 随后读取这个数据。如果 T1 撤销了这次修改，那么 T2 读取的数据是脏数据。 -
+
## 不可重复读 T2 读取一个数据，T1 对该数据做了修改。如果 T2 再次读取这个数据，此时读取的结果和第一次读取的结果不同。 -
+
## 幻影读 T1 读取某个范围的数据，T2 在这个范围内插入新的数据，T1 再次读取这个范围的数据，此时读取的结果和和第一次读取的结果不同。 -
+
---- @@ -541,7 +541,7 @@ Entity-Relationship，有三个组成部分：实体、属性、联系。 - [The basics of the InnoDB undo logging and history system](https://blog.jcole.us/2014/04/16/the-basics-of-the-innodb-undo-logging-and-history-system/) - [MySQL locking for the busy web developer](https://www.brightbox.com/blog/2013/10/31/on-mysql-locks/) - [浅入浅出 MySQL 和 InnoDB](https://draveness.me/mysql-innodb) -- [Innodb 中的事务隔离级别和锁的关系](https://tech.meituan.com/innodb-lock.html) +- [Innodb 中的事务隔离级别和锁的关系](https://tech.meituan.com/2014/08/20/innodb-lock.html) --- diff --git "a/convert/\346\236\204\345\273\272\345\267\245\345\205\267.md" "b/convert/\346\236\204\345\273\272\345\267\245\345\205\267.md" index 3dc1f5e..4c357ba 100644 --- "a/convert/\346\236\204\345\273\272\345\267\245\345\205\267.md" +++ "b/convert/\346\236\204\345\273\272\345\267\245\345\205\267.md" @@ -32,7 +32,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 主要包括 Ant、Maven 和 Gradle。 -
+
Gradle 和 Maven 的区别是，它使用 Groovy 这种特定领域语言（DSL）来管理构建脚本，而不再使用 XML 这种标记性语言。因为项目如果庞大的话，XML 很容易就变得臃肿。 diff --git "a/convert/\346\266\210\346\201\257\351\230\237\345\210\227.md" "b/convert/\346\266\210\346\201\257\351\230\237\345\210\227.md" index a457573..a708c4f 100644 --- "a/convert/\346\266\210\346\201\257\351\230\237\345\210\227.md" +++ "b/convert/\346\266\210\346\201\257\351\230\237\345\210\227.md" @@ -10,20 +10,21 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 消息生产者向消息队列中发送了一个消息之后，只能被一个消费者消费一次。 -
+
## 发布/订阅 消息生产者向频道发送一个消息之后，多个消费者可以从该频道订阅到这条消息并消费。 -
+
发布与订阅模式和观察者模式有以下不同： - 观察者模式中，观察者和主题都知道对方的存在；而在发布与订阅模式中，发布者与订阅者不知道对方的存在，它们之间通过频道进行通信。 - 观察者模式是同步的，当事件触发时，主题会调用观察者的方法，然后等待方法返回；而发布与订阅模式是异步的，发布者向频道发送一个消息之后，就不需要关心订阅者何时去订阅这个消息，可以立即返回。 -
+
+ # 二、使用场景 diff --git "a/convert/\347\256\227\346\263\225.md" "b/convert/\347\256\227\346\263\225.md" index 604f046..eec6ff2 100644 --- "a/convert/\347\256\227\346\263\225.md" +++ "b/convert/\347\256\227\346\263\225.md" @@ -260,7 +260,7 @@ public abstract class Sort> { 选择排序需要 \~N2/2 次比较和 \~N 次交换，它的运行时间与输入无关，这个特点使得它对一个已经排序的数组也需要这么多的比较和交换操作。 -
+
```java public class Selection> extends Sort { @@ -287,9 +287,7 @@ public class Selection> extends Sort { 在一轮循环中，如果没有发生交换，就说明数组已经是有序的，此时可以直接退出。 -以下演示了在一轮循环中，将最大的元素 5 上浮到最右侧。 - -
+
```java public class Bubble> extends Sort { @@ -325,7 +323,7 @@ public class Bubble> extends Sort { 以下演示了在一轮循环中，将元素 2 插入到左侧已经排序的数组中。 -
+
```java public class Insertion> extends Sort { @@ -350,7 +348,7 @@ public class Insertion> extends Sort { 希尔排序使用插入排序对间隔 h 的序列进行排序。通过不断减小 h，最后令 h=1，就可以使得整个数组是有序的。 -
+
```java public class Shell> extends Sort { @@ -384,7 +382,7 @@ public class Shell> extends Sort { 归并排序的思想是将数组分成两部分，分别进行排序，然后归并起来。 -
+
### 1. 归并方法 @@ -411,7 +409,7 @@ public abstract class MergeSort> extends Sort { } else if (j > h) { nums[k] = aux[i++]; - } else if (aux[i].compareTo(nums[j]) <= 0) { + } else if (aux[i].compareTo(aux[j]) <= 0) { nums[k] = aux[i++]; // 先进行这一步，保证稳定性 } else { @@ -479,7 +477,7 @@ public class Down2UpMergeSort> extends MergeSort { - 归并排序将数组分为两个子数组分别排序，并将有序的子数组归并使得整个数组排序； - 快速排序通过一个切分元素将数组分为两个子数组，左子数组小于等于切分元素，右子数组大于等于切分元素，将这两个子数组排序也就将整个数组排序了。 -
+
```java public class QuickSort> extends Sort { @@ -510,7 +508,7 @@ public class QuickSort> extends Sort { 取 a[l] 作为切分元素，然后从数组的左端向右扫描直到找到第一个大于等于它的元素，再从数组的右端向左扫描找到第一个小于它的元素，交换这两个元素。不断进行这个过程，就可以保证左指针 i 的左侧元素都不大于切分元素，右指针 j 的右侧元素都不小于切分元素。当两个指针相遇时，将切分元素 a[l] 和 a[j] 交换位置。 -
+
```java private int partition(T[] nums, int l, int h) { @@ -614,7 +612,7 @@ public T select(T[] nums, int k) { 堆可以用数组来表示，这是因为堆是完全二叉树，而完全二叉树很容易就存储在数组中。位置 k 的节点的父节点位置为 k/2，而它的两个子节点的位置分别为 2k 和 2k+1。这里不使用数组索引为 0 的位置，是为了更清晰地描述节点的位置关系。 -
+
```java public class Heap> { @@ -650,7 +648,7 @@ public class Heap> { 在堆中，当一个节点比父节点大，那么需要交换这个两个节点。交换后还可能比它新的父节点大，因此需要不断地进行比较和交换操作，把这种操作称为上浮。 -
+
```java private void swim(int k) { @@ -663,7 +661,7 @@ private void swim(int k) { 类似地，当一个节点比子节点来得小，也需要不断地向下进行比较和交换操作，把这种操作称为下沉。一个节点如果有两个子节点，应当与两个子节点中最大那个节点进行交换。 -
+
```java private void sink(int k) { @@ -712,15 +710,13 @@ public T delMax() { 无序数组建立堆最直接的方法是从左到右遍历数组进行上浮操作。一个更高效的方法是从右至左进行下沉操作，如果一个节点的两个节点都已经是堆有序，那么进行下沉操作可以使得这个节点为根节点的堆有序。叶子节点不需要进行下沉操作，可以忽略叶子节点的元素，因此只需要遍历一半的元素即可。 -
+
#### 5.2 交换堆顶元素与最后一个元素 交换之后需要进行下沉操作维持堆的有序状态。 -
- -
+
```java public class HeapSort> extends Sort { @@ -2013,7 +2009,7 @@ public class Transaction { 对于 N 个键，M 条链表 (N>M)，如果哈希函数能够满足均匀性的条件，每条链表的大小趋向于 N/M，因此未命中的查找和插入操作所需要的比较次数为 \~N/M。 -
+
### 3. 线性探测法 @@ -2021,7 +2017,7 @@ public class Transaction { 使用线性探测法，数组的大小 M 应当大于键的个数 N（M>N)。 -
+
```java public class LinearProbingHashST implements UnorderedST { @@ -2122,7 +2118,7 @@ public void delete(Key key) { 线性探测法的成本取决于连续条目的长度，连续条目也叫聚簇。当聚簇很长时，在查找和插入时也需要进行很多次探测。例如下图中 2\~5 位置就是一个聚簇。 -
+
α = N/M，把 α 称为使用率。理论证明，当 α 小于 1/2 时探测的预计次数只在 1.5 到 2.5 之间。为了保证散列表的性能，应当调整数组的大小，使得 α 在 [1/4, 1/2] 之间。 diff --git "a/convert/\350\256\241\347\256\227\346\234\272\346\223\215\344\275\234\347\263\273\347\273\237.md" "b/convert/\350\256\241\347\256\227\346\234\272\346\223\215\344\275\234\347\263\273\347\273\237.md" index e4a3a31..d93b11b 100644 --- "a/convert/\350\256\241\347\256\227\346\234\272\346\223\215\344\275\234\347\263\273\347\273\237.md" +++ "b/convert/\350\256\241\347\256\227\346\234\272\346\223\215\344\275\234\347\263\273\347\273\237.md" @@ -12,7 +12,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 并发是指宏观上在一段时间内能同时运行多个程序，而并行则指同一时刻能运行多个指令。 -并行需要硬件支持，如多流水线或者多处理器。 +并行需要硬件支持，如多流水线、多核处理器或者分布式计算系统。 操作系统通过引入进程和线程，使得程序能够并发运行。 @@ -32,7 +32,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 多个进程能在同一个处理器上并发执行使用了时分复用技术，让每个进程轮流占有处理器，每次只执行一小个时间片并快速切换。 -虚拟内存使用了空分复用技术，它将物理内存抽象为地址空间，每个进程都有各自的地址空间。地址空间和物理内存使用页进行交换，地址空间的页并不需要全部在物理内存中，当使用到一个没有在物理内存的页时，执行页面置换算法，将该页置换到内存中。 +虚拟内存使用了空分复用技术，它将物理内存抽象为地址空间，每个进程都有各自的地址空间。地址空间的页被映射到物理内存，地址空间的页并不需要全部在物理内存中，当使用到一个没有在物理内存的页时，执行页面置换算法，将该页置换到内存中。 ### 4. 异步 @@ -835,7 +835,9 @@ FIFO 常用于客户-服务器应用程序中，FIFO 用作汇聚点，在客户 举例：一个系统为某进程分配了三个物理块，并有如下页面引用序列： -
$7，0，1，2，0，3，0，4，2，3，0，3，2，1，2，0，1，7，0，1$

+$$ +7，0，1，2，0，3，0，4，2，3，0，3，2，1，2，0，1，7，0，1 +$$ 开始运行时，先将 7, 0, 1 三个页面装入内存。当进程要访问页面 2 时，产生缺页中断，会将页面 7 换出，因为页面 7 再次被访问的时间最长。 @@ -849,7 +851,9 @@ FIFO 常用于客户-服务器应用程序中，FIFO 用作汇聚点，在客户 因为每次访问都需要更新链表，因此这种方式实现的 LRU 代价很高。 -
$4，7，0，7，1，0，1，2，1，2，6$

+$$ +4，7，0，7，1，0，1，2，1，2，6 +$$
diff --git "a/convert/\350\256\241\347\256\227\346\234\272\347\275\221\347\273\234.md" "b/convert/\350\256\241\347\256\227\346\234\272\347\275\221\347\273\234.md" index b91bc3c..c1d7165 100644 --- "a/convert/\350\256\241\347\256\227\346\234\272\347\275\221\347\273\234.md" +++ "b/convert/\350\256\241\347\256\227\346\234\272\347\275\221\347\273\234.md" @@ -16,19 +16,21 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 互联网服务提供商 ISP 可以从互联网管理机构获得许多 IP 地址，同时拥有通信线路以及路由器等联网设备，个人或机构向 ISP 缴纳一定的费用就可以接入互联网。 -
+
目前的互联网是一种多层次 ISP 结构，ISP 根据覆盖面积的大小分为第一层 ISP、区域 ISP 和接入 ISP。互联网交换点 IXP 允许两个 ISP 直接相连而不用经过第三个 ISP。 -
+
## 主机之间的通信方式 - 客户-服务器（C/S）：客户是服务的请求方，服务器是服务的提供方。 +
+ - 对等（P2P）：不区分客户和服务器。 -
+
## 电路交换与分组交换 @@ -46,7 +48,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 总时延 = 排队时延 + 处理时延 + 传输时延 + 传播时延 -
+
### 1. 排队时延 @@ -60,7 +62,9 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 主机或路由器传输数据帧所需要的时间。 -
$delay=\frac{l(bit)}{v(bit/s)}$

+$$ +delay=\frac{l(bit)}{v(bit/s)} +$$ 其中 l 表示数据帧的长度，v 表示传输速率。 @@ -68,17 +72,20 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 电磁波在信道中传播所需要花费的时间，电磁波传播的速度接近光速。 -
$delay=\frac{l(m)}{v(m/s)}$

+$$ +delay=\frac{l(m)}{v(m/s)} +$$ 其中 l 表示信道长度，v 表示电磁波在信道上的传播速度。 ## 计算机网络体系结构 -
+
+ ### 1. 五层协议 -- **应用层** ：为特定应用程序提供数据传输服务，例如 HTTP、DNS 等。数据单位为报文。 +- **应用层** ：为特定应用程序提供数据传输服务，例如 HTTP、DNS 等协议。数据单位为报文。 - **传输层** ：为进程提供通用数据传输服务。由于应用层协议很多，定义通用的传输层协议就可以支持不断增多的应用层协议。运输层包括两种协议：传输控制协议 TCP，提供面向连接、可靠的数据传输服务，数据单位为报文段；用户数据报协议 UDP，提供无连接、尽最大努力的数据传输服务，数据单位为用户数据报。TCP 主要提供完整性服务，UDP 主要提供及时性服务。 @@ -104,7 +111,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF TCP/IP 体系结构不严格遵循 OSI 分层概念，应用层可能会直接使用 IP 层或者网络接口层。 -
+
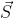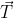### 4. 数据在各层之间的传递过程 @@ -194,21 +201,27 @@ TCP/IP 体系结构不严格遵循 OSI 分层概念，应用层可能会直接 ### 5. 码分复用 -为每个用户分配 m bit 的码片，并且所有的码片正交，对于任意两个码片 $\vec{S}$ 和 $\vec{T}$ 有 +为每个用户分配 m bit 的码片，并且所有的码片正交，对于任意两个码片 和 有 -
$\frac{1}{m}\vec{S}\cdot\vec{T}=0$

+$$ +\frac{1}{m}\vec{S}\cdot\vec{T}=0 +$$ -为了讨论方便，取 m=8，设码片 $\vec{S}$ 为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片，发送比特 0 时就发送该码片的反码 11100100。 +为了讨论方便，取 m=8，设码片 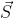为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片，发送比特 0 时就发送该码片的反码 11100100。 在计算时将 00011011 记作 (-1 -1 -1 +1 +1 -1 +1 +1)，可以得到 -
$\frac{1}{m}\vec{S}\cdot\vec{S}=1$

+$$ +\frac{1}{m}\vec{S}\cdot\vec{S}=1 +$$ -
$\frac{1}{m}\vec{S}\cdot\vec{S'}=-1$

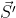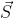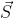+$$ +\frac{1}{m}\vec{S}\cdot\vec{S'}=-1 +$$ -其中 $\vec{S'}$ 为 $\vec{S}$ 的反码。 +其中 为 的反码。 -利用上面的式子我们知道，当接收端使用码片 $\vec{S}$ 对接收到的数据进行内积运算时，结果为 0 的是其它用户发送的数据，结果为 1 的是用户发送的比特 1，结果为 -1 的是用户发送的比特 0。 +利用上面的式子我们知道，当接收端使用码片 对接收到的数据进行内积运算时，结果为 0 的是其它用户发送的数据，结果为 1 的是用户发送的比特 1，结果为 -1 的是用户发送的比特 0。 码分复用需要发送的数据量为原先的 m 倍。 @@ -281,7 +294,7 @@ MAC 地址是链路层地址，长度为 6 字节（48 位），用于唯一标 正是由于这种自学习能力，因此交换机是一种即插即用设备，不需要网络管理员手动配置交换表内容。 -下图中，交换机有 4 个接口，主机 A 向主机 B 发送数据帧时，交换机把主机 A 到接口 1 的映射写入交换表中。为了发送数据帧到 B，先查交换表，此时没有主机 B 的表项，那么主机 A 就发送广播帧，主机 C 和主机 D 会丢弃该帧。主机 B 向主机 A 发送数据包时，交换机查找交换表得到主机 A 映射的接口为 1，就发送数据帧到接口 1，同时交换机添加主机 B 到接口 3 的映射。 +下图中，交换机有 4 个接口，主机 A 向主机 B 发送数据帧时，交换机把主机 A 到接口 1 的映射写入交换表中。为了发送数据帧到 B，先查交换表，此时没有主机 B 的表项，那么主机 A 就发送广播帧，主机 C 和主机 D 会丢弃该帧，主机 B 回应该帧向主机 A 发送数据包时，交换机查找交换表得到主机 A 映射的接口为 1，就发送数据帧到接口 1，同时交换机添加主机 B 到接口 2 的映射。
@@ -608,13 +621,19 @@ TCP 使用超时重传来实现可靠传输：如果一个已经发送的报文 一个报文段从发送再到接收到确认所经过的时间称为往返时间 RTT，加权平均往返时间 RTTs 计算如下： -
$RTTs=(1-a)*(RTTs)+a*RTT$

+$$ +RTTs=(1-a)*(RTTs)+a*RTT +$$ + +其中，0 ≤ a ＜ 1，RTTs 随着 a 的增加更容易受到 RTT 的影响。 超时时间 RTO 应该略大于 RTTs，TCP 使用的超时时间计算如下： -
$RTO=RTTs+4*RTT_d$

+$$ +RTO=RTTs+4*RTT_d +$$ -其中 RTTd 为偏差。 +其中 RTTd 为偏差的加权平均值。 ## TCP 滑动窗口 diff --git "a/convert/\351\233\206\347\276\244.md" "b/convert/\351\233\206\347\276\244.md" index 46d4bc7..74cfe4f 100644 --- "a/convert/\351\233\206\347\276\244.md" +++ "b/convert/\351\233\206\347\276\244.md" @@ -6,16 +6,16 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF # 一、负载均衡 -集群中的应用服务器（节点）通常被设计成无状态，用户可以请求任何一个应用服务器。 +集群中的应用服务器（节点）通常被设计成无状态，用户可以请求任何一个节点。 负载均衡器会根据集群中每个节点的负载情况，将用户请求转发到合适的节点上。 负载均衡器可以用来实现高可用以及伸缩性： - 高可用：当某个节点故障时，负载均衡器会将用户请求转发到另外的节点上，从而保证所有服务持续可用； -- 伸缩性：根据系统整体负载情况，可以很容易地添加移除节点。 +- 伸缩性：根据系统整体负载情况，可以很容易地添加或移除节点。 -负载均衡运行过程包含两个部分： +负载均衡器运行过程包含两个部分： 1. 根据负载均衡算法得到转发的节点； 2. 进行转发。 @@ -28,11 +28,11 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 下图中，一共有 6 个客户端产生了 6 个请求，这 6 个请求按 (1, 2, 3, 4, 5, 6) 的顺序发送。(1, 3, 5) 的请求会被发送到服务器 1，(2, 4, 6) 的请求会被发送到服务器 2。 -
+
该算法比较适合每个服务器的性能差不多的场景，如果有性能存在差异的情况下，那么性能较差的服务器可能无法承担过大的负载（下图的 Server 2）。 -
+
### 2. 加权轮询（Weighted Round Robbin） @@ -40,7 +40,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 例如下图中，服务器 1 被赋予的权值为 5，服务器 2 被赋予的权值为 1，那么 (1, 2, 3, 4, 5) 请求会被发送到服务器 1，(6) 请求会被发送到服务器 2。 -
+
### 3. 最少连接（least Connections） @@ -48,27 +48,25 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 例如下图中，(1, 3, 5) 请求会被发送到服务器 1，但是 (1, 3) 很快就断开连接，此时只有 (5) 请求连接服务器 1；(2, 4, 6) 请求被发送到服务器 2，只有 (2) 的连接断开，此时 (6, 4) 请求连接服务器 2。该系统继续运行时，服务器 2 会承担过大的负载。 -
+
最少连接算法就是将请求发送给当前最少连接数的服务器上。 例如下图中，服务器 1 当前连接数最小，那么新到来的请求 6 就会被发送到服务器 1 上。 -
+
### 4. 加权最少连接（Weighted Least Connection） 在最少连接的基础上，根据服务器的性能为每台服务器分配权重，再根据权重计算出每台服务器能处理的连接数。 -
- ### 5. 随机算法（Random） 把请求随机发送到服务器上。 和轮询算法类似，该算法比较适合服务器性能差不多的场景。 -
+
### 6. 源地址哈希法 (IP Hash) @@ -76,7 +74,7 @@ PDF制作github: https://github.com/sjsdfg/CS-Notes-PDF 可以保证同一 IP 的客户端的请求会转发到同一台服务器上，用来实现会话粘滞（Sticky Session） -
+
## 转发实现 @@ -91,7 +89,7 @@ HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服 该负载均衡转发的缺点比较明显，实际场景中很少使用它。 -
+
### 2. DNS 域名解析 @@ -107,7 +105,7 @@ HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服 大型网站基本使用了 DNS 做为第一级负载均衡手段，然后在内部使用其它方式做第二级负载均衡。也就是说，域名解析的结果为内部的负载均衡服务器 IP 地址。 -
+
### 3. 反向代理服务器 @@ -164,7 +162,7 @@ HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服 - 当服务器宕机时，将丢失该服务器上的所有 Session。 -
+
## Session Replication @@ -175,7 +173,7 @@ HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服 - 占用过多内存； - 同步过程占用网络带宽以及服务器处理器时间。 -
+
## Session Server @@ -189,7 +187,7 @@ HTTP 重定向负载均衡服务器使用某种负载均衡算法计算得到服 - 需要去实现存取 Session 的代码。 -
+
参考：