recurrent

Keras recurrent tutorial

This section will walk you through the code of recurrent_keras_power.py which I suggest you have open while reading.

This tutorial is mostly homemade, however inspired from Daniel Hnyk's blog post

The dataset we'll be using can be downloaded there : https://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption#. It is a 20 Mo zip file containing a text file.

The task here will be to be able to predict values for a timeseries : the history of 2 million minutes of a household's power consumption. We are going to use a multi-layered LSTM recurrent neural network to predict the last value of a sequence of values. Put another way, given 49 timesteps of consumption, what will be the 50th value?

Recurrent Keras power

Table Of Content

#General oragnization

We start with importing everything we'll need (no shit...). Then we define functions to load the data, compile the model, train it and plot the results.

The overall philosophy is modularity. We use default parameters in the run_network function so that you can feed it with already loaded data (and not re-load it each time you train a network) or a pre-trained network model to enable warm restarts.

Imports

import matplotlib.pyplot as plt
import numpy as np
import time
import csv
from keras.models import Sequential
from keras.layers.core import Dense, Activation, Dropout
from keras.layers.recurrent import LSTM
np.random.seed(1234)

• matplotlib, numpy, time are pretty straight forward.

• csv is a module that will be used to load the data from the txt file.

• models is the core of Keras's neural networks implementation. It is the object that represents the network : it will have layers, activations and so on. It is the object that will be 'trained' and 'tested'. Sequetial means we will use a 'layered' model, not a graphical one.

• Dense, Activation, Dropout core layers are used to build the network : feedforward standard layers and Activation and Dropout modules to parametrize the layers.

• LSTM is a reccurent layer. LSTM cells are quite complex and should be carefully studied (see in resources: Chris Olah's Understanding LSTM Networks and N. De Freitas's video), however see here the default parameters.

Last thing is that for reproductibility, a seed is used in numpy's random.

Loading the data

def data_power_consumption(path_to_dataset='household_power_consumption.txt', sequence_length=50, ratio=1.0):

    max_values = ratio * 2049280
    
    with open(path_to_dataset) as f:
        data = csv.reader(f, delimiter=";")
        power = []
        nb_of_values = 0
        for line in data:
            try:
                power.append(float(line[2]))
                nb_of_values += 1
            except ValueError:
                pass
            # 2049280.0 is the total number of valid values, i.e. ratio = 1.0
            if nb_of_values / 2049280.0 >= ratio:
                break

The initial file contains lots of different pieces of data. We will here focus on a single value : a house's Global_active_power history, minute by minute for almost 4 years. This means roughly 2 million points. Some values are missing, this is why we try to load the values as floats into the list and if the value is not a number ( missing values are marked with a ?) we simply ignore them.

Also if we do not want to load the entire dataset, there is a condition to stop loading the data when a certain ratio is reached.

    result = []
    for index in range(len(power) - sequence_length):
        result.append(power[index: index + sequence_length])
    result = np.array(result)  # shape (2049230, 50)

Once all the datapoints are loaded as one large timeseries, we have to split it into examples. Again, one example is made of a sequence of 50 values. Using the first 49, we are going to try and predict the 50th. Moreover, we'll do this for every minute given the 49 previous ones so we use a sliding buffer of size 50.

    result_mean = result.mean()
    result -= result_mean
    print "Shift : ", result_mean
    print "Data  : ", result.shape

Neural networks usually learn way better when data is pre-processed (cf Y. Lecun's 1995 paper, section 4.3). However regarding time-series we do not want the network to learn on data too far from the real world. So here we'll keep it simple and simply center the data to have a 0 mean.

    row = int(round(0.9 * result.shape[0]))
    train = result[:row, :]
    np.random.shuffle(train)
    X_train = train[:, :-1]
    y_train = train[:, -1]
    X_test = result[row:, :-1]
    y_test = result[row:, -1]

Now that the examples are formatted, we need to split them into train and test, input and target. Here we select 10% of the data as test and 90% to train. We also select the last value of each example to be the target, the rest being the sequence of inputs.

We shuffle the training examples so that we train in no particular order and the distribution is uniform (for the batch calculation of the loss) but not the test set so that we can visualize our predictions with real signals.

    X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))
    X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
    
    return [X_train, y_train, X_test, y_test]

Last thing regards input formats. Read through the recurrent post to get more familiar with data dimensions. So we reshape the inputs to have dimensions (#examples, #values in sequences, dim. of each value). Here each value is 1-dimensional, they are only one measure (of power consumption at time t). However if we were to predict speed vectors they could be 3 dimensional for instance.

In fine, we return X_train, y_train, X_test, y_test in a list (to be able to feed it as one only object to our run function)

Building the model

def build_model():

    model = Sequential()
    layers = [1, 50, 100, 1]

So here we are going to build our Sequential model. This means we're going to stack layers in this object.

Also, layers is the list containing the sizes of each layer. We are therefore going to have a network with 1-dimensional input, two hidden layers of sizes 50 and 100 and eventually a 1-dimensional output layer.

    model.add(LSTM(
            layers[1],
            input_shape=(None, 1),
            return_sequences=True))
    model.add(Dropout(0.2))

After the model is initialized, we create a first layer, in this case an LSTM layer. Here we use the default parameters so it behaves as a standard recurrent layer. Since our input is of 1 dimension, we declare that it should expect an input_dim of 1. Then we say we want layers[1] units in this layer. We also add 20% Dropout in this layer.

    model.add(LSTM(
            layers[2],
            return_sequences=False))
    model.add(Dropout(0.2))

Second layer is even simpler to create, we just say how many units we want (layers[2]) and Keras takes care of the rest.

    model.add(Dense(
            layers[3]))
    model.add(Activation("linear"))

The last layer we use is a Dense layer ( = feedforward). Since we are doing a regression, its activation is linear.

    start = time.time()
    model.compile(loss="mse", optimizer="rmsprop")
    print "Compilation Time : ", time.time() - start
    return model

Lastly, we compile the model using a Mean Square Error (again, it's standard for regression) and the RMSprop optimizer. See the mnist example to learn more on rmsprop.

Return_Sequence

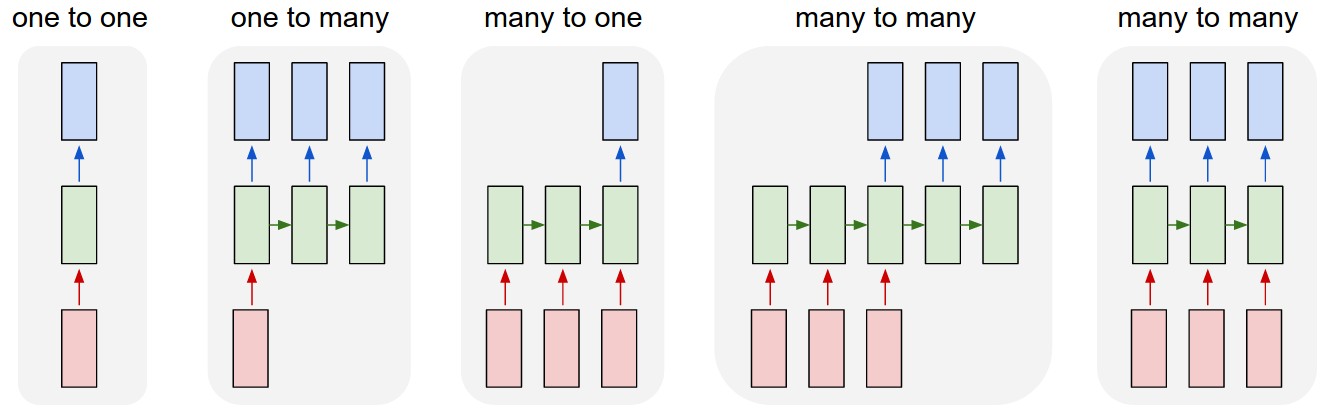
For now we have not looked into the return_sequence= parameter of the LSTM layers. Just like in the recurrent post on dimensions, we'll use Andrej Karpathy's chart to understand what is hapenning. See the post for more details on how to read it.

The difference between return_sequence=True and return_sequence=False is that in the first case the network behaves as in the 5th illustration (second many to many) and in the latter it behaves as the 3rd, many to one.

In our case, the first LSTM layer returns sequences because we want it to transfer its information both to the next layer (upwards in the chart) and to itself for the next timestep (arrow to the right).

However for the second one, we just expect its last sequence prediction to be compared to the target. This means for inputs 0 to sequence_length - 2 the prediction is only passed to the layer itself for the next timestep and not as an input to the next ( = output) layer. However the sequence_length - 1th input is passed forward to the Dense layer for the loss computation against the target.

More details?

If you're still not clear with what happens, let's set sequence_length to 3. In this case the aim would be to predict the 4th value and compute the loss against the real 4th value, the target.

1. The first example value is fed to the network from the input

   a. The first hidden layer's activation is computed and passed both to the second hidden layer and to itself

   b. The second hidden layer takes as input the first hidden layer's activation, computes its own activation and passes it only to itself

2. The second example of the same sequence is fed from the input

   a. The first hidden layer takes as input both this value and its own previous prediction from the first timestep. The computed activation is fed again both to the second layer and to the first hidden layer itself

   b. The second layer behaves likewise: it takes its previous prediction and the first hidden layer's output as inputs and outputs an activation. This activation, once again, is fed to the second hidden layer for the next timestep

3. The last value of the sequence is input into the network

   a. The first hidden layer behaves as before (2.a)

   b. The second layer also behaves as before (2.b) except that this time, its activation is also passed to the last, Dense layer.

   c. The Dense layer computes its activation from the second hidden layer's activation. This activation is the prediction our network does for the 4th timestep.

To conclude, the fact that return_sequence=True for the first layer means that its output is always fed to the second layer. As a whole regarding time, all its activations can be seen as the sequence of prediction this first layer has made from the input sequence.
On the other hand, return_sequence=False for the second layer because its output is only fed to the next layer at the end of the sequence. As a whole regarding time, it does not output a prediction for the sequence but one only prediction-vector (of size layer[2]) for the whole input sequence. The linear Dense layer is used to aggregate all the information from this prediction-vector into one single value, the predicted 4th timestep of the sequence.

To go further

Had we stacked three recurrent hidden layers, we'd have set return_sequence=True to the second hidden layer and return_sequence=False to the last. In other words, return_sequence=False is used as an interface from recurrent to feedforward layers (dense or convolutionnal).

Also, if the output had a dimension > 1, we'd only change the size of the Dense layer.

Running the network

def run_network(model=None, data=None):
    global_start_time = time.time()
    epochs = 1
    ratio = 0.5
    sequence_length = 50
    path_to_dataset = 'household_power_consumption.txt'
    
    if data is None:
        print 'Loading data... '
        X_train, y_train, X_test, y_test = data_power_consumption(
                path_to_dataset, sequence_length, ratio)
    else:
        X_train, y_train, X_test, y_test = data
    
    print '\nData Loaded. Compiling...\n'
    
    if model is None:
        model = build_model()

Just like before, to be as modular as possible we start with checking whether or not data and model values were provided. If not we load the data and build the model. Set ratio to the proportion of the entire dataset you want to load (of course ratio <= 1 ... if not data_power_consumption will behave as if ratio = 1)

    try:
        model.fit(
            X_train, y_train,
            batch_size=512, nb_epoch=epochs, validation_split=0.05)
        predicted = model.predict(X_test)
        predicted = np.reshape(predicted, (predicted.size,))
    except KeyboardInterrupt:
        print 'Training duration (s) : ', time.time() - global_start_time
        return model, y_test, 0

Again, we put the training into a try/except statement so that we can interrupt the training without losing everything to a KeyboardInterrupt.

To train the model, we call the model's fit method. Nothing new here. Pretty straight forward.

Let's focus a bit on predicted.

• by construction X_test is an array with 49 columns (timesteps). The list [ X_test[i][0] ] is the entire signal (minus the last 49 values) from which it was built since we've used a 1-timestep sliding buffer.

• X_test[0] is the first sequence, that is to say the first 49 values of the original signal.

• predict(X_test[0]) is therefore the prediction for the 50th value and its associated target is y_test[0]. Moreover, by construction, y_test[0] = X_test[1][48] = X_test[2][47] = ...

• then predict(X_test[1]) is the prediction of the 51th value, associated with y_test[1] as a target.

• therefore predict(X_test) is the predicted signal, one step ahead, and y_test is its target.

• predict(X_test) is a list of lists (in fact a 2-dimensional numpy array) with one value, therefore we reshape it so that it simply is a list of values (1-dimensional numpy array).

In case of keyboard interruption, we return the model, y_test and X_test. The latter is returned so that you can run predict on the early-returned model if you like.

    try:
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.plot(y_test[:100, 0])
        plt.plot(predicted[:100, 0])
        plt.show()
    except Exception as e:
        print str(e)
    print 'Training duration (s) : ', time.time() - global_start_time
    return model, y_test, predicted

Lastly we plot the result of the prediction for the first 100 timesteps and return model, y_test and the predicted values.