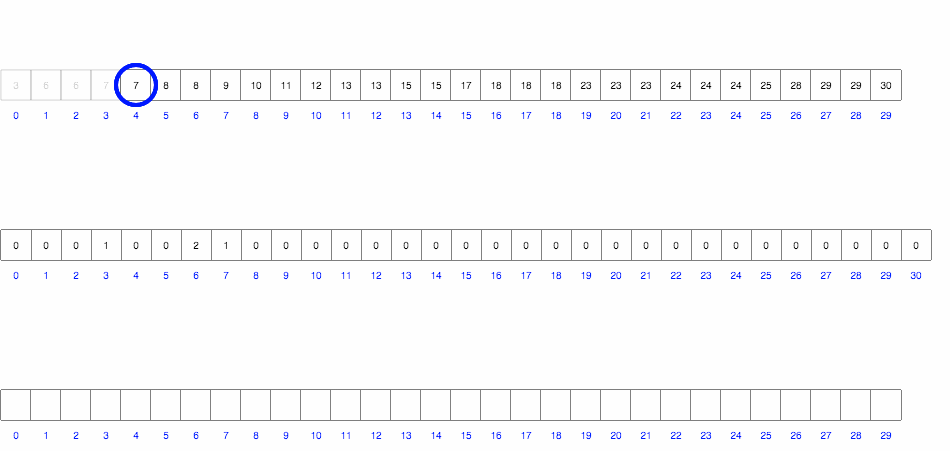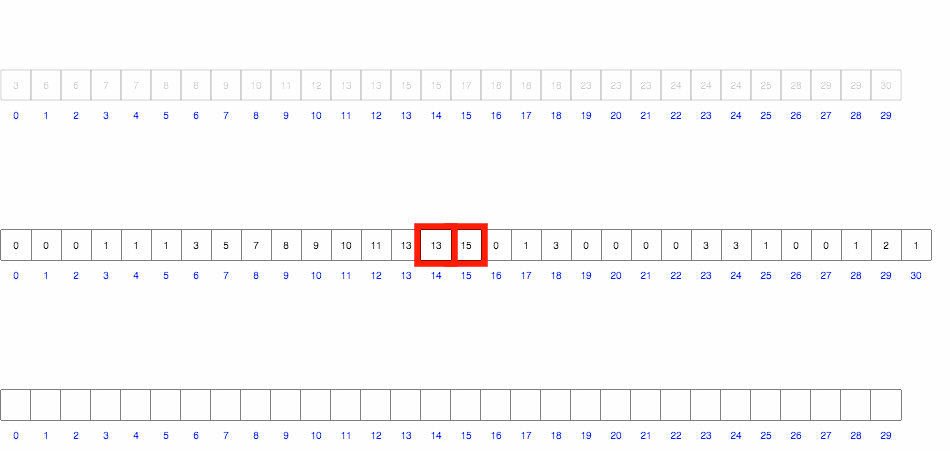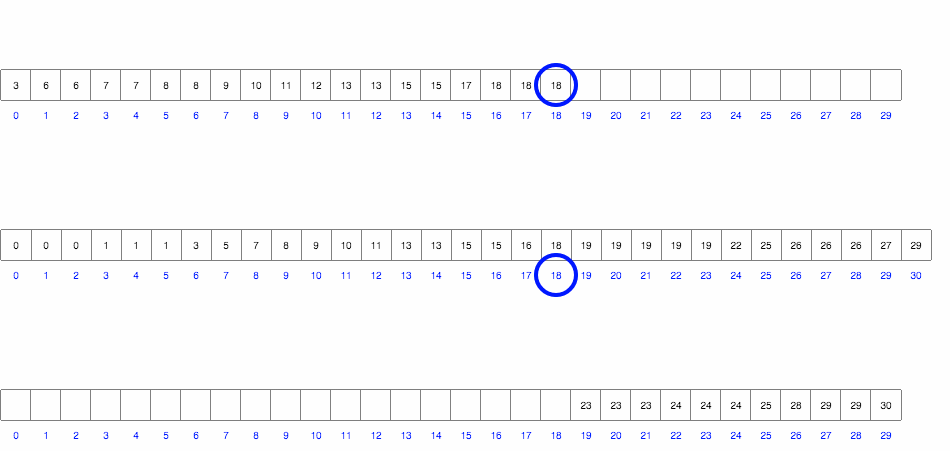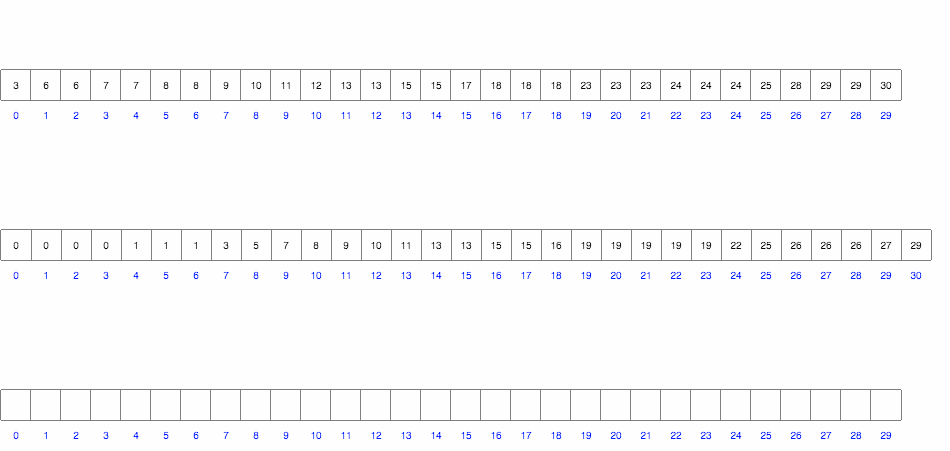
традиционные алгоритмы сортировки массивов написанные на Swift 4
Выбираем некоторый опорный элемент (например, средний). После этого разбиваем исходный массив на три части: элементы эквивалентные опорному, меньше, больше опорного. Рекурсивно вызовемся от большей и меньшей частей. В итоге получим отсортированный массив, так как каждый элемент меньше опорного стоял раньше каждого большего опорного.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n2) | O(n log n) | O(n) |
| худший случай: если опорный элемент наименьший или наибольший из всех, то каждый раз массив разбивается на подмассивы размерами 1 и n-1 | - | лучший случай: массив постоянно разбивается опорным элементом на две раные части |
Расход памяти: В общем случае O(log n). При неудачных подборках опорного элемнта O(n) - здесь память будет расходоваться не на создание новых вспомогательных массивов, а на рекурсию, хранение адресов возврата и локальных переменных.
Алгоритм неустойчив (неудачные входные данные могут привести к значительному увеличению времени работы и расхода памяти). Является одним из самых быстродействующих алгоритмов, однако для массивов с небольшим количеством элементом может оказаться малоэффективным.
Алгоритм пробегает по всем ещё не упорядоченным элементам, ищет среди них минимальный (сохраняя его значение и индекс) и переставляет в конец выстриваемого списка.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n2) | O(n2) | O(n2) |
Расход памяти: O(1). Дополнительной памяти не требуется.
Алгоритм неустойчив.
Соседние элементы сравниваются и при необходимости меняются местами, в результате "лёгкие" элементы перемещаются к началу списка, а "тяжёлые" - к концу. Операция циклически выполняется для оставшихся элементов.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n2) | O(n2) | O(n) |
Расход памяти: O(1). Дополнительной памяти не требуется.
Алгоритм устойчив. На практике может использоваться лишь для сортировки маленьких массивов. И в этом случае лучше взять классическую сортировку, а не её модификацию.
Устанавливаем левую и правую границы сортируемой области массива. Поочерёдно просматриваем массив справа налево и слева направо. На очередной итерации при достижении правой границы сдвигаем её на предыдущий элемент (-1) и движемся справа налево, при достижении левой границы сдвигаем её на следующий элемент (+1) и двигаемся слева направо.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n2) | зависит от выбранных шагов | O(n log2 n) |
| худший случай: отсортированный в обратном порядке массив | - | лучший случай: отсортированный массив |
Расход памяти: O(1). Дополнительной памяти не требуется.
Алгоритм устойчив.
Сравниваем элементы находящиеся друг от друга на некотором расстоянии (шаге). В алгоритме два цикла. Внутренний переставляет элементы. Внешний служит для изменения шага, через который внутренний цикл элементы будет переставлять. Шаг постепенно сокращается до 1 (минимальное расстояние между двумя элементами) - и тогда алгоритм Шелла превращается в обычную сортировку вставками.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n2) | O(n2) | O(n) |
| худший случай: неудачный выбор шага | - | лучший случай: массив уже отсортирован в правильном порядке |
Расход памяти: O(1). Дополнительной памяти не требуется.
Алгоритм неустойчив.
Проходимся по массиву и подсчитываем количество вхождений каждого элемента. После проходим по массиву значений и выводим каждое число столько раз, сколько нужно.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n) | O(n) | O(n) |
Расход памяти: O(1). Дополнительной памяти не требуется.
Алгоритм устойчив. Применение сортировки подсчётом целесообразно лишь тогда, когда массив состоит из целочисленных, положительных чисел.
Исходный массив делится надвое на всё меньшие подмассивы, пока количество элементов в очередных не станет равным 2 или 1. Если в подмассиве 2 элемента, то он упорядочивается банальным сравнением. А подмассив из одного элемента по своей сути является упорядоченным. Затем происходит обратный процесс - слияние подмассивов. Поскольку подмассивы к этому времени являются упорядоченными, то можем сравнивать лишь элементы, стоящие в их начале.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n log n) | O(n log n) | O(n log n) |
Расход памяти: O(n). Требует дополнительной памяти, примерно равной размеру исходного массива. Память расходуется на рекурсивный вызов и на постоянное создание вспомогательных подмассивов.
Алгоритм устойчив. На «почти отсортированных» массивах работает столь же долго, как на хаотичных.
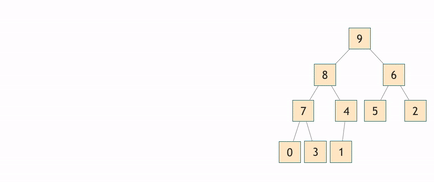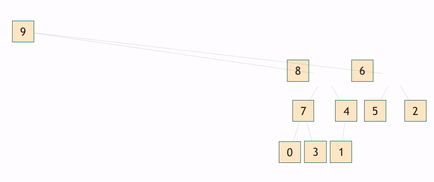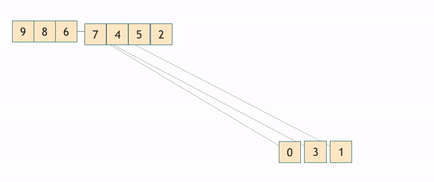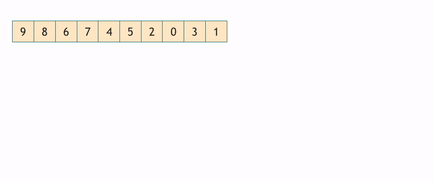
Строим на основе неотсортированного массива так называемую двоичную кучу или пирамиду. В результате получается бинарное дерево каждый узел которого больше предыдущего, тем самым на вершине дерева оказывается элемент с максимальным значением. Затем вершина дерева переставляется в конец, откуда и будет выстраиваться отсортированный подмассив. А среди оставшихся элементов происходит ряд перестановок с целью восстановить дерево, чтобы в его вершине вновь оказался максимальный элемент из ещё не отсортированной части. Таким образом на первом месте постоянно оказывается один из самых "лёгких" элементов, который затем серией перестановок отправляется назад.
Асимптотика:
| сложность в худшем | сложность в среднем | сложность в лучшем |
|---|---|---|
| O(n log n) | O(n log n) | O(n log n) |
Расход памяти: O(1). Дополнительной памяти не требуется. Хотя в алгоритме присутствует рекурсивный вызов, но чтобы добраться до конца даже очень большого массива, рекурсий нужно мало, и они моментально закрываются.
Алгоритм устойчив. На почти отсортированных массивах работает столь же долго, как и на хаотических данных. Не работает на связанных списках и других структурах памяти последовательного доступа. Из-за сложности реализации выигрыш получается только на больших размерах массива.
- Сортировка расческой / Comb sort
- Сортировка вставками / Insertion sort
- Сортировка двоичным деревом / Tree sort
- Гномья сортировка / Gnome sort
- Блочная сортировка / Bucket sort
- Поразрядная сортировка / Radix sort
- Битонная сортировка / Bitonic sort
- реализовать гибридную сортировку