The purpose of the DM-AM model is to determine the density of Black Woodpeckers that is necessary to supply enough caves for a population of feral Western Honey Bees to be viable in an average german forest.
- bwps: Pairs of Black Woodpeckers (Dryocopus martius L.)
- hbs: Swarms of Western Honey Bees (Apis mellifera L.)
- hives: Boxes, in which Honey Bee colonies are held domestically by beekeepers
- caves: Tree cavities built by bwps
- target: possible patches to fly to and potentially build next cave
- pot-homes: all unoccupied caves or hives, that are at least the minimum swarming distance and at most the maximum swarming distance away
- target: the 1 potential home, that lies closest to the preferred swarming distance
- parent: the hive or cave, the swarm originates from
- free?: determines, if a hive is free or occupied
- grade: quality of the hive from a bee colonies perspective
- mortality-rate: probability of a colony to die
same as hives +
- age: time since the cave was produced
- Grain: 1 month
- Extent: until Honey Bees have gone extinct
- Grain: 1 ha (100 m * 100 m)
- Extent: 26 km^2 (5.1 km * 5.1 km)
Because processes happen in a yearly cycle, ticks are assigned months. Following this, processes happen only in specific months. The model starts with January (tick 0). Which agent sets are affected by which process is described in Chapter Sub-models.
- January: kill-bees
- April: produce-caves
- May: swarm
- June: swarm
- October: weather
- December: destroy
The simulation stops when the Honey Bee population has gone extinct.
The DM-AM model features essentially two relationships:
- The relationship of the Woodpecker density on the density of tree cavities
- The relationship of the density of tree cavities on the viability of the feral Honey Bee population.
Both relationships are coupled in this model through A -> B -> C.
The validity of the model depends on the hypothesis, that caves are at the moment the main limiting factor of feral Honey Bee viability. All other limiting factors like food resources and parasitic load (Varroa destructor) have therefore been neglected from the model. Both could later be implemented using a density regulation.
Viability is understood in the way, that the feral Honey Bee colonies can sustain the population on their own, i.e. without the support of the domesticated colonies (which are usually reinstated every year). Therefore, all domesticated bee colonies are removed in the model after 100 years, so the viability of the feral colonies can be monitored. 100 years is chosen, because under all combinations of parameters, the system has reached equilibrium until then.
The results show that, as expected, with more Woodpeckers, more caves emerge, and therefore the Honey Bee population is more viable.
For the model results to be interpreted properly, a follow up population viability analysis (PVA) has to be done. The goal is to find the density of Woodpeckers, for which at least 95% of Honey Bee populations last for at least 100 years after the hives have been removed.
Sensing appears in the form of the swarms finding possible homes around them. In reality, scouting bees would explore the surrounding and lead the swarm to the best fit based on a democratic process. This is modelled by assuming, the swarm senses all possible homes within the maximum swarming distance (and outside the minimum swarming distance).
Swarms interact only indirectly by competing for possible homes to move into. In denser areas, the competition is higher by logic, because multiple swarms select the same free homes and have the same ones close to their preferred distance.
The following processes are include random choices:
- Where woodpeckers and caves are placed (inside the forest)
- Where beekeepers are located (outside the forest)
- Which of their surrounding cells contain a hive
- The initial ages of caves
- Which one out of multiple candidates moves into a free home
- If a cave gets destroyed in December
- If a cave or hive releases a swarm
Except for the ages of initial caves, which are drawn from an exponential distribution, all random processes are drawn from the uniform distribution.
- In the upper right corner of the arena and right next to it, there are a month and a year counter, to track when changes are happening. (Those counters are realized via a helper agent-set and and a common monitor respectively)
- Two plots are used to monitor the amount of caves in total and those who are occupied, and the ratio of occupied over all caves. In both, a vertical line is drawn at the moment when the hives are removed
- The shape of hives and caves is determined by their state of occupation (free?) and shows a big Honey Bee on top of it if occupied
- If a switch is activated, lines are drawn, were swarms fly. Swarms originating from hives draw black lines, from caves yellow lines
The forest is a square of side length 3.1km placed in the center of the arena. All area around the forest (ring of width 1km) is farmland / urban. This is realized using a boolean forest? and the patch color.
The following parameters are needed for initialization:
- Density of woodpecker pairs: 0.1 - 1.1 / km^2 (Abs et al 1980) (this is the main input parameter)
- Number of beekeepers: 6 (derived from average beekeeper density in Germany (Deutscher Imkerbund, 2024)
- Number of beehives: 46 (derived from average beehive density in Germany (BMEL, 2024)
- Minimum swarming distance: 200 m
- Maximum swarming distance: 1000 m
- Preferred swarming distance: 450 m (all three derived from swarming preferences in Seeley & Morse, 1977 and Kohl & Rutschmann 2018)
- Probability of a woodpecker pair to produce a cave per year: 15 % (Abs et al 1980)
-
Out of the density of woodpecker pairs, an absolute number is calculated using the area of the forest.
-
The initial number of caves distributed in the forest is induced by the number of woodpeckers using the following quadratic equation. The equation results from a linear model, which was fitted on data by Zahner et al 2017, Abs et al 1980, Hoffmann 2005, and Müller 2013:
f(x) = -0.42x2+9.3x
- To guarantee, that the increment and the decay of caves are balanced out, the cave mortality is induced from the cave production probability per woodpecker pair, and the caves per woodpecker using the following equation:
cave-mortality = (cave-prod-prob / initial-number-caves * number-bwps)
- Woodpeckers and caves are placed in the forest
- Beekeepers and therefore the hives are placed in the farmland / urban area
- The hives are distributed as clusters of radius 300m around the beekeepers but strictly outside the forest
The age distribution of caves follows the exponential distribution which is parameterized using the cave mortality:
set age random-exponential (1 / cave-mortality)
Honey Bee colonies die of harsh conditions with a probability determined by the grade of their hive or cave by the following equation:
mortality-rate [%] = 100 - grade
All Woodpeckers fly to a random forest patch and with a probability of 15% produce a new empty cave.
In May, the swarm procedure works as follows:
- 95% of hives whose colony has died in the most recent January get restocked with a new colony (common practice in bee-keeping).
- All caves and hives release a swarm with the probability [%] of their grade.
- Now all swarms look for possible free homes in a range of specified distances (described in Initialization). They select the one possible free home that is closest to their preferred swarming distance and fly there. If only one swarm flew to this free home, it can move in. If multiple swarms candidate for this home, one gets chosen randomly to move in. All others return back to their origin for then possible free homes are recalculated and the next most preferred free home is flewn to. This process repeats 3 times. Swarms, that at this point still haven't found a home to move into, die.
In June, the swarm-procedure skips the first step. In the second step, the probability to release a swarm is halved. The rest is the same. This is based on personal experience of Honey Bee swarming behaviour.
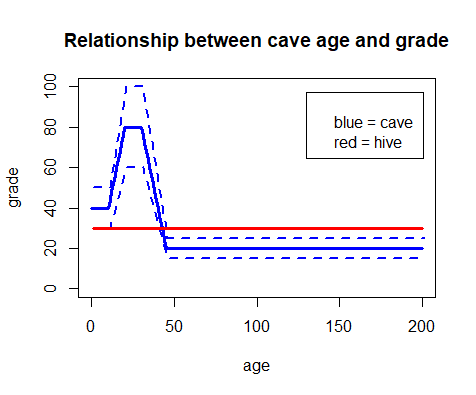
All caves age by 1 year. Using that age, the grade is calculated following the below shown hump-shaped non-linear relationship (blue).
Hives don't weather and therefore keep a constant grade of 30 (shown in green). The dashed lines show the margin of uncertainty, which is tested using a sensitivity analysis. This uncertainty is a factor (0.75 - 1.25), which scales the grade.
With a probabity of cave-mortality, a cave gets destroyed during a winter storm.
-
Hoffmann, M. (2005). Der Schwarzspecht (Dryocopus martius) im Burgwald–Bestandsentwicklung, Brutbaumauswahl und Höhlenanlage. Zeitschrift Für Vogelkunde Und Naturschutz in Hessen. Vogel Und Umwelt, 16, 67–91.
-
Kohl, P. L., & Rutschmann, B. (2018). The neglected bee trees: European beech forests as a home for feral honey bee colonies. PeerJ, 6, e4602. https://doi.org/10.7717/peerj.4602
-
Müller, J. (2013). Schwarzspecht Dryocopus martius und Mittelspecht Dendrocopos medius als Leitarten für den Waldnaturschutz in der Vorbergzone des Nordschwarzwaldes. https://www.ogbw.de/images/ogbw/files/orn_jh/29/02_MuellerWaldvoegel.pdf
-
Seeley, T. D., & Morse, R. A. (1977). Dispersal Behavior of Honey Bee Swarms. Psyche: A Journal of Entomology, 84, 199–209. https://doi.org/10.1155/1977/37918
-
Zahner, V., Bauer, R., & Kaphegyi, T. A. M. (2017). Are Black Woodpecker (Dryocopus martius) tree cavities in temperate Beech (Fagus sylvatica) forests an answer to depredation risk? Journal of Ornithology, 158(4), 1073–1079. https://doi.org/10.1007/s10336-017-1467-2
-
Bundesanstalt für Landwirtschaft und Ernährung. (1. Mai, 2024). Anzahl der Bienenvölker in Deutschland in den Jahren 2007 bis 2023 (in 1.000) [Graph]. In Statista. Zugriff am 22. Juli 2024, von https://de.statista.com/statistik/daten/studie/487925/umfrage/bienenvoelker-in-deutschland/
-
Deutscher Imkerbund. (1. März, 2024). Anzahl der Imker in Deutschland nach Landesverbänden des Imkerbundes im Jahr 2023 [Graph]. In Statista. Zugriff am 22. Juli 2024, von https://de.statista.com/statistik/daten/studie/1085577/umfrage/anzahl-der-imker-in-deutschland-nach-regionen/