Symbolica ⊆ Modern Computer Algebra

Symbolica is a blazing fast computer algebra system for Python and Rust, born of a need to push the boundaries of computations in science and enterprise. Check out the live Jupyter Notebook demo!

For documentation and more, see symbolica.io.

Quick Example

Symbolica allows you to build and manipulate mathematical expressions, for example from a Jupyter Notebook:

You are able to perform these operations from the comfort of a programming language that you (probably) already know, by using Symbolica's bindings to Python and Rust:

Installation

Visit the Get Started page for detailed installation instructions.

Python

Symbolica can be installed for Python >3.5 using pip:

pip install symbolica

Rust

If you want to use Symbolica as a library in Rust, simply include it in the Cargo.toml:

[dependencies]
symbolica = "0.14"

Examples

Below we list some examples of the features of Symbolica. Check the guide for a complete overview.

Pattern matching

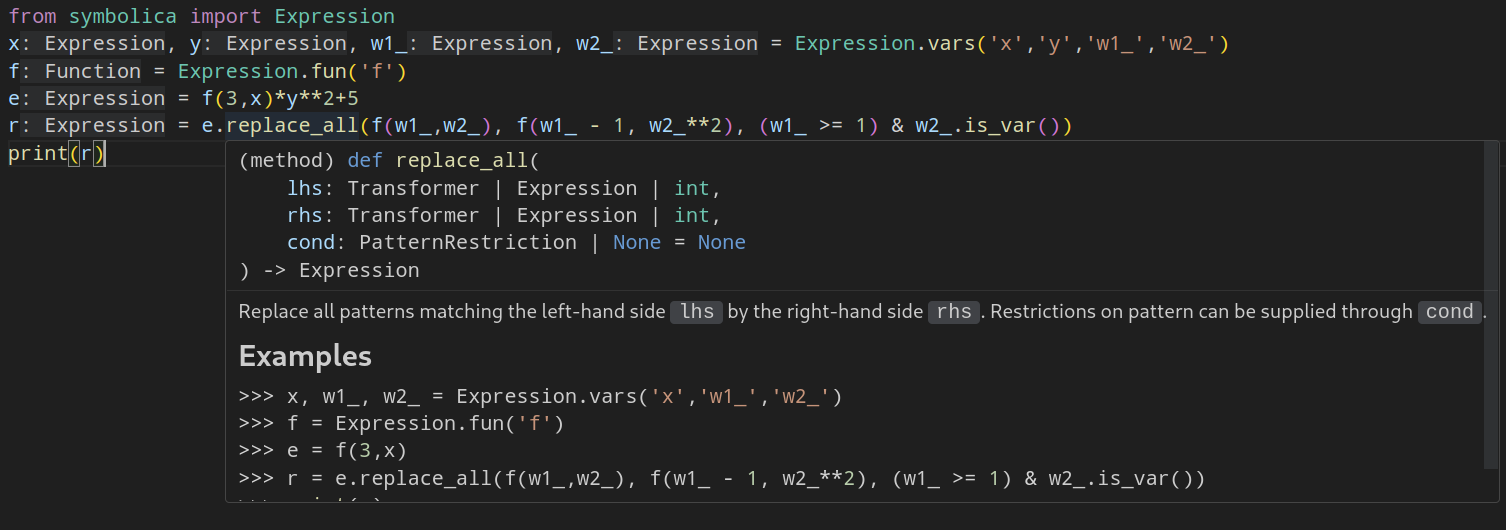
Variables ending with a _ are wildcards that match to any subexpression. In the following example we try to match the pattern f(w1_,w2_):

from symbolica import *
x, y, w1_, w2_, f = S('x','y','w1_','w2_', 'f')
e = f(3,x)*y**2+5
r = e.replace_all(f(w1_,w2_), f(w1_ - 1, w2_**2))
print(r)

which yields y^2*f(2,x^2)+5.

Solving a linear system

Solve a linear system in x and y with a parameter c:

from symbolica import *

x, y, c, f = S('x', 'y', 'c', 'f')

x_r, y_r = Expression.solve_linear_system(
    [f(c)*x + y + c, y + c**2], [x, y])
print('x =', x_r, ', y =', y_r)

which yields x = (-c+c^2)*f(c)^-1 and y = -c^2.

Series expansion

Perform a series expansion in x:

from symbolica import *
e = E('exp(5+x)/(1-x)').series(S('x'), 0, 3)

print(e)

which yields (exp(5))+(2*exp(5))*x+(5/2*exp(5))*x^2+(8/3*exp(5))*x^3+𝒪(x^4).

Rational arithmetic

Symbolica is world-class in rational arithmetic, outperforming Mathematica, Maple, Form, Fermat, and other computer algebra packages. Simply convert an expression to a rational polynomial:

from symbolica import *
p = E('(x*y^2*5+5)^2/(2*x+5)+(x+4)/(6*x^2+1)').to_rational_polynomial()
print(p)

which yields (45+13*x+50*x*y^2+152*x^2+25*x^2*y^4+300*x^3*y^2+150*x^4*y^4)/(5+2*x+30*x^2+12*x^3).

Development

Follow the development and discussions on Zulip!